As a rigid body moves through space the particles that make up that rigid body can see two different type of motion, translation, and rotation about a fixed axis, or a combination of the two. For right now I am first going to discuss translation.
Translation is a straight forward type of motion. The particles of a rigid body will all follow paths that are parallel to each other. These paths could be straight or they could be curved. Another aspect of translation is all particles will see the same acceleration. Due to this fact the same principles that were used to determine the forces on a particle can be used to determine the forces on a rigid body.
Eq 1 $\sum{}F_x=m(a_G)_x$
Eq 2 $\sum{}F_y=m(a_G)_y$
Eq 3 $\sum{}F_z=m(a_G)_x$
However, since this a rigid body, there will be a center of mass $G$. As a result, if the resulting moments caused by the forces in the x, y, and z direction do not cancel each other out, the body will start to rotate around its center of mass. Once the body starts to rotate, the problem will no longer just have translation, it will also have rotation about a fixed axis. Resulting in the fixed axis is going through the center of mass of the rigid body. Consequently, to prevent this from happening the sum of the moments around the center of mass must equal zero.
Eq 4 $\sum{}M_{G_x}=0$
Eq 5 $\sum{}M_{G_y}=0$
Eq 6 $\sum{}M_{G_z}=0$
As a result even if you believe that you are trying to solve a problem that only has translation. You must still analyze the moments around the center of mass to make sure that all of the moments will cancel out. Otherwise the rigid body will start to rotate around its center of mass.
Example
A car is accelerating at 1.85 $\frac{m}{s^2}$. Its mass is 1800 kg and the car is rear wheel drive. The cars center of mass is located at point G. What is the force applied to the back and front wheel as the car accelerates?
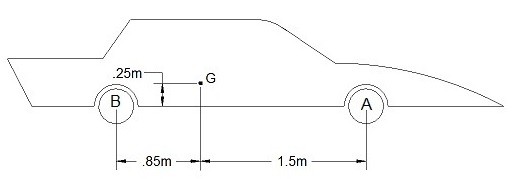
Solution
The first step to solving any type of rigid body problem is to draw a free body diagram so that you can visually account for all of the different forces.
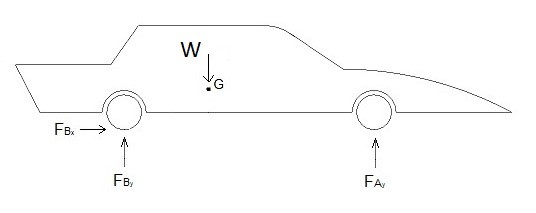
Next, you need to write out the equations of motion. Since this a 2d problem, you will only need to consider the forces in the x and y direction, and moments caused by those forces around the z axis of the center of mass.
$W = 1800~kg(9.81\frac{m}{s^2}=17.7~kN$
$\sum{}F_x=ma_x=1800~kg(1.85~\frac{m}{s^2}+F_{B_x} = 3.33 kN+F_{B_x}=0$
$\sum{}F_y = ma_y= F_{A_y}+F_{B_y}-17.7~kN=0$
$\sum{}M_{G_z}=0=.25F_{B_x}-.85F_{B_y}+1.5F_{A_y}$
Finally, solve for $F_{A_y}$, $F_{B_x}$, and $F_{B_y}$.
$F_{A_y}=6.73~kN$
$F_{B_x}=-3.33~kN$
$F_{B_y}=10.97~kN$