A 3-dimensional rigid body has six degrees of freedom. It can translate in the x, y, and z directions. In addition, the rigid body can rotate on the x, y, and z axis. If the motion does not have any type of translational acceleration than there will be no force in the x, y, or z direction. Also, there will be no moment around the x, y, or z axis if there is no angular acceleration. However, if there are, and it’s a combination of translational acceleration and angular acceleration, the rigid body will develop General Plane Forces & Moments.
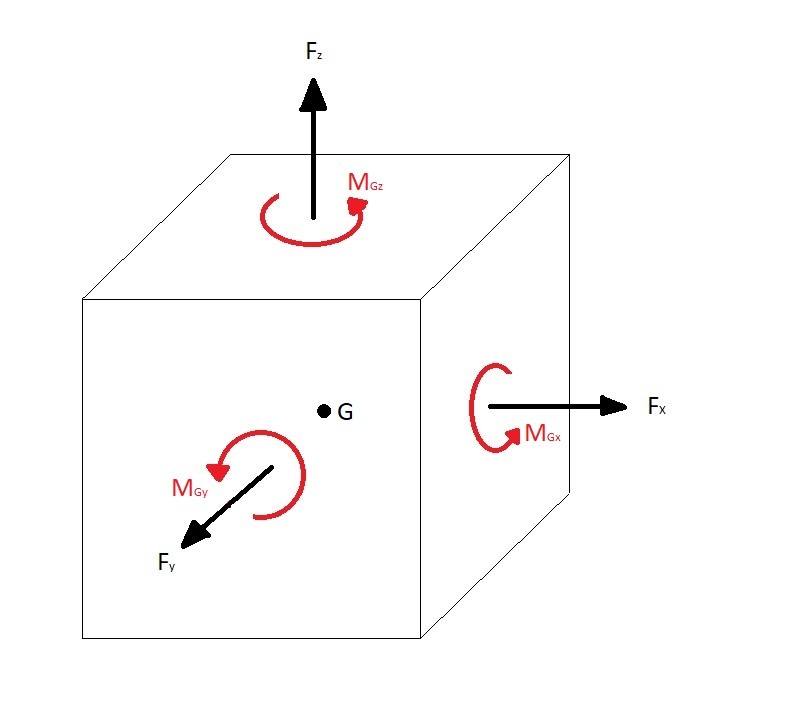
(Eq 1) $\sum{}F_x=m(a_{Gx})$, $\sum{}F_y=m(a_{Gy})$, $\sum{}F_z=m(a_{Gz})$
(Eq 2) $\sum{}M_{Gx}=I_xα_x$ , $\sum{}M_{Gy}=I_yα_y$, $\sum{}M_{Gz}=I_zα_z$
Generally, when defining your coordinate system you will want to have the x, y, and z axis go through the point of zero rotation. You should determine the sum of the moments on each axis based off of this point. Also, the translational forces will not be effected by the normal or tangential rotational forces at the point of zero rotation. Generally, unless forced to do otherwise, a rigid body will rotate around its center of mass G.
Frictional Rolling
Another type of problem that could have general plane forces & moments is a rotating wheel that is creating a force to move an object. To move the object the wheel will need to generate a force that will be dependent on friction.
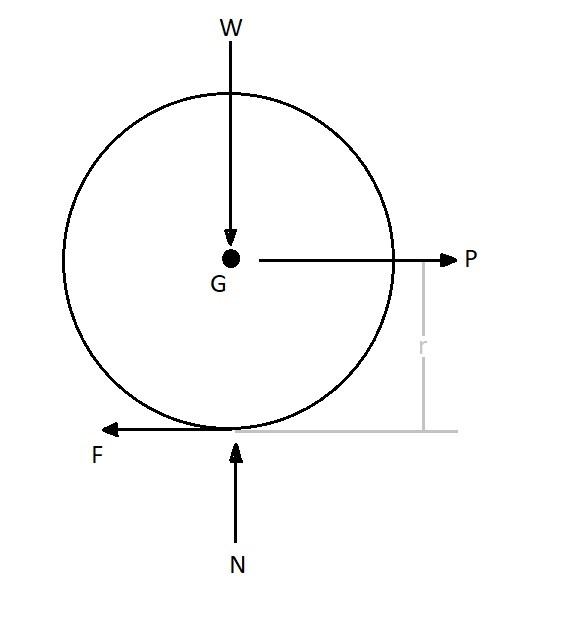
Above is a typical free body diagram of a wheel that is generating a force to move an object. The frictional force is represented by F, and the variable P is the force being placed on the object to move it. In addition the variable W is weight pressing down on the wheel. While N represents the counter force pressing up on the wheel. The resulting equations of motion can be seen bellow.
(Eq 3) $\sum{}F_x=ma_{Gx}=P-F$
(Eq 4) $\sum{}F_y=0=N-W$
(Eq 5) $\sum{}M_{Gz}=-Fr=I_{Gz}α$
You should notice that there will are currently 4 unknowns with only 3 equations to solve for them. Due to this you will need to know whether the wheel has no slip or if it is slipping to determine what the fourth equation would be to find all of the unknowns. If the wheel has no slip than through kinematics you can relate $a_{Gx}$ to $α$ using the following equation.
(Eq 6) $a_{Gx}=αr$
On the other hand if the wheel is slipping than you will need to know what the coefficient of kinetic friction is between the two surfaces. Once you know what the coefficient of kinetic friction is you can relate the frictional force F to the force N by using the following equation.
(Eq 7) $ F=μ_kN$