In a previous article I talked about forces on a rigid body in respect to translational motion. However, besides translation, a rigid body could also have rotational forces due to rotation about a fixed axis. Rotation about a fixed axis means that there will be no movement in the x, y, or z directions while the body rotates on an axis perpendicular to a plane.
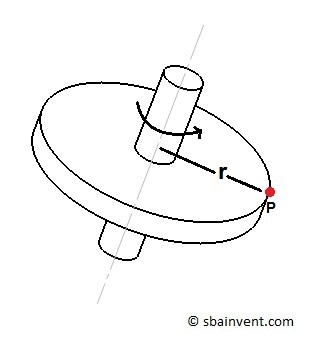
Rotation Around the Center of Mass
As a rigid body rotates about its center of mass there will be always be a normal force that will steadily increase as you move away from the center of mass. However, there will be no normal force at the point of rotation. The sum of all of normal forces on each particle will equal zero if the body is rotating around its center of mass. A body that is rotating around its center of mass is balanced.
(Eq 1) $F_n=ma_n=mϖ^2r$
If the body has a change in angular velocity an angular acceleration will result causing a tangential force. As with normal force tangential force will increase the further the point of analysis is from the axis of rotation. In addition to tangential force, there will also be a resultant moment that is the product of the mass moment of inertia of the rigid body and the angular acceleration.
(Eq 2) $F_t=ma_t=mαr$
(Eq 3) $∑M_G=I_Gα$
where
$m$ = mass
$ϖ$ = angular velocityI
$α$ = angular acceleration
$I_G$ = mass moment of inertia of the rigid body
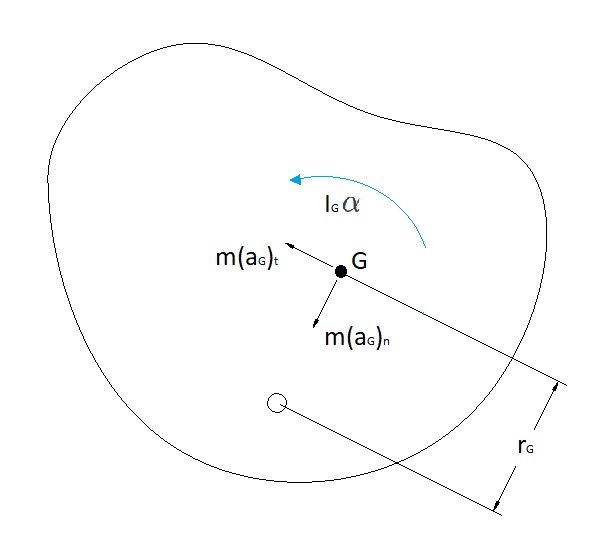
Axis of rotation offset from the Center of Mass
There could also be cases where the axis of rotation is not going through the center of mass. This would create a rotation that is out of balance. Meaning that the sum of the normal forces will not cancel each other out. Instead on one side of the rigid body there will be a maximum normal force and the other side a minimum normal force. The difference between these force will cause a resulting force that the axis will have to restrain to keep the rigid body from moving the x, or z direction.
An example of this is when you car’s wheels aren’t balanced correctly. As your car is moving it will feel like you are going over a series of bumps on the road. The force of these bumps will become worse as you pick up speed. This is do to the normal forces not canceling each other out due to the wheel not being in balance. This can be calculated by finding the normal force at the center of mass in respect to the axis of rotation by using the following equation.
(Eq 4) $\sum{}F_n=ma_{G_n}=mϖ^2r_G$
Notice that the above equation is just a modified version of equation 1.
Another aspect that is affected would be the moment around the axis of rotation. The mass moment of inertia would not equal the mass moment of inertia of the rigid body around the center of mass. Instead the mass moment of inertia would have to be calculated using the parallel axis theorem as seen below.
(Eq 5) $I_O=I_G+md^2$
where
$d$ = the distance the center of mass is from the center of rotation
From this equation 3 can be modified to the following.
(Eq 6) $∑M_O=I_Oα=\sum{}F_t(r_g)+I_Gα$
where
(Eq 7) $\sum{}F_t=ma_{G_t}=mαr_G$
Example
A pulley with a uniform mass of 22kg has a force of 15 N hung from it on a chord. Determine the forces on the axle holding the pulley, and determine the angular velocity after 5 second of rest. The pulley is initially at rest.
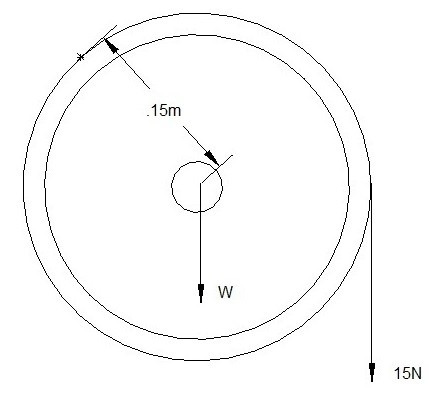
Solution
Step 1: The first step is to draw a free body diagram. Since the axle is in the center of pulley, and the mass of the pulley is uniform, it can be assumed the center of mass is located at the axis of rotation.
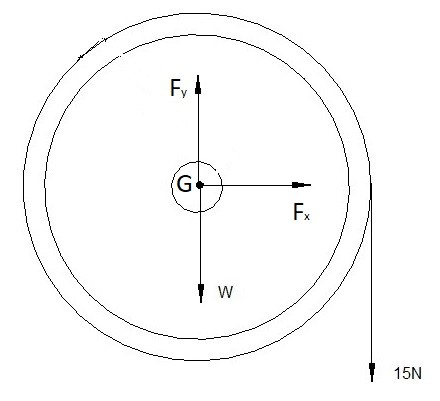
Step 2: Since the center of mass is on the axis of rotation the tangential force and normal force on the center of mass will be zero. The forces on the pulley will be caused by its weight and the 15 N weight.
$\sum{}F_x=ma_x=0$
$\sum{}F_y=ma_y=F_y-W-15=0$
$W=22(9.81) = 215.8~N$
$F_y=230.8~N$
Step 3: To determine the angular velocity of the pulley after 5 second you will first need to determine the angular acceleration cause by the 15 N weight on the pulley. To do that you will need to use equation 3.
$∑M_G=I_Gα$
$M=.15(15)=2.25~N·m$
$I=\frac{1}{2}mr^2$$=\frac{1}{2}(22)(.15)^2=0.25~kg·m^2$
$α=\frac{M}{I}=\frac{2.25}{0.25}=9\frac{rad}{s^2}$
Now that the angular acceleration has been determine the angular velocity can now be determine.
$ϖ=αt=9(5)=45\frac{rad}{s}$