Statically Indeterminate Axial Loading

A statically indeterminate problem is a problem that can’t be solved using statics equations alone, since there will be more unknown variables than there are statics equations to solve for. Most cases in a real word situation are statically indeterminate. For a member that is axial loaded in one direction, there is only one static equation that can be used to solve for the unknowns. If the situation is similar to the figure below then it would be considered statically indeterminate.

The above image is statically indeterminate because both ends of the part are fixed. This would result in an unknown force on both faces which I am calling force F_A and force F_B. Now to satisfy the statics equation so that the forces sum to zero we would have to use the following equation.

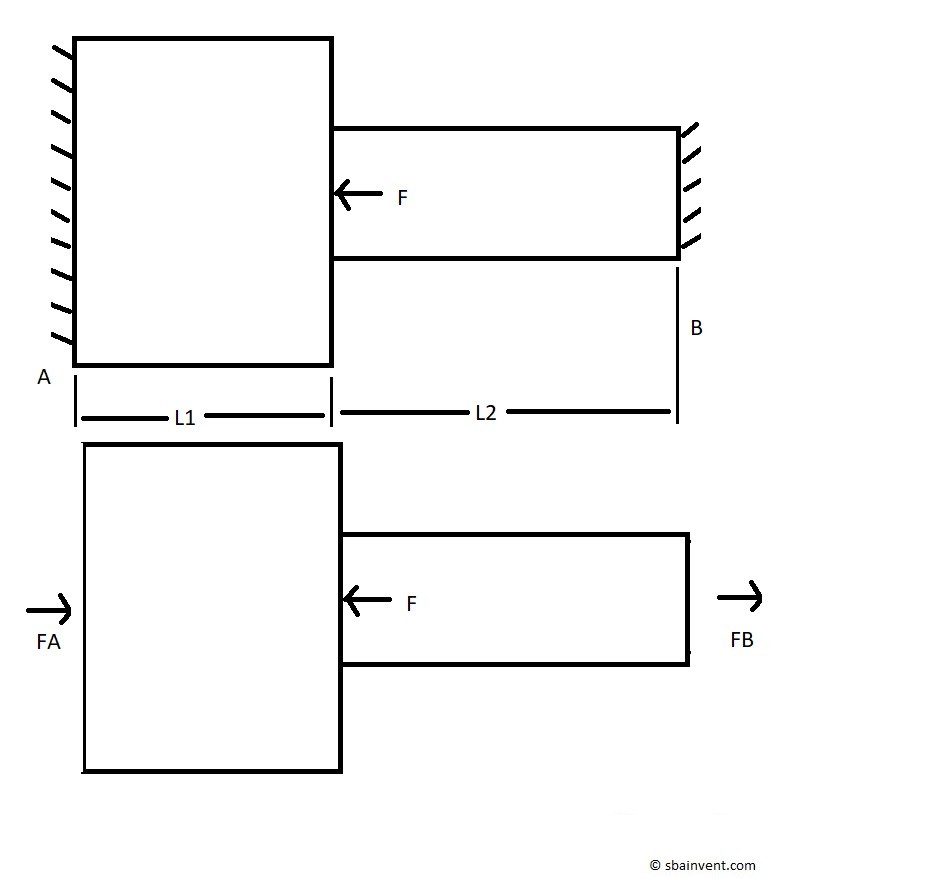
(Eq 1)  $F_A+F_B-F=0$

From the above equation it can be seen that there are more variables than unknowns. This makes this problem statically indeterminate.

So how can we solve for the force on each wall if we have too many variables to do so? Well remember that Hook’s Law is used relate stress and strain by using young’s modulus. So this will result in the following equation.

(Eq 2)  $Δδ_1+Δδ_2=\frac{-F_AL_1}{E_1A_1}+\frac{F_BL_2}{E_2A_2}=0$

F_A is negative due to it being a compressive load.

To simplify the above equation and make it easier to solve I’m going to do the following.

(Eq 3)  $C=\frac{L_1}{E_1A_1},~D=\frac{L_2}{E_2A_2}$

This will simplify equation 2 to the following.

(Eq 4)  $-F_AC+F_BD=0$

Now we can solve equation 1 for F_A.

(Eq 5)  $F_A=F-F_B$

Now supplementing equation 5 into equation 3 we can solve for F_B.

(Eq 6)  $F_B=F\left(\frac{C}{C+D} \right)$

Finally, F_A can now be found using equation 7.

(Eq 7)  $F_A=F\left(1-\frac{C}{C+D}\right)$