Through most of this section I have discussed Hook’s Law and how it applies to the Young’s Modulus of a material. Young’s Modulus, however, is only used for normal stresses and strains. What about if that object is in shear. If that is the case than instead of using Young’s Modulus the Shear Modulus would be used.
The shear modulus follows the same principles as Young’s Modulus. It is based off the same exact stress or strain curve as seen below. Accept instead of using stresses and strains that would be considered normal, which would typically be pushing or pulling forces. The stress and strain are shear stress and shear strain.
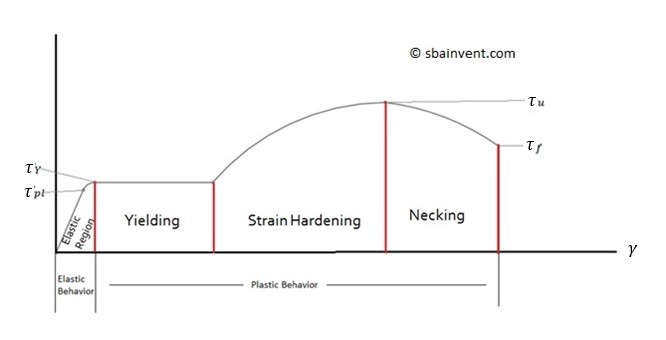
The elastic region of the curve would then be represented by the following equation.
(Eq 1) $τ=Gγ$
τ = shear stress
γ = shear strain
G = Shear Modulus
Now, what if you know what the Young’s Modulus of the material is but you don’t know what the Shear modulus is, you can use the Poisson’s Ratio to find the Shear modulus. To do this use the following equation.
(Eq 2) $G=\frac{E}{2(1+ν)}$
ν = Poisson’s Ratio
G = Shear Modulus
Now each material has a unique Poisson’s Ratio which can be found by looking up the material properties. However, if you don’t have access to this most material have a Poisson’s ratio is normally around 0.3 for most metals.
Finally, what exactly is Poisson’s Ratio? Simply, Poisson’s ratio is the ratio of transverse strain over longitudinal or axial strain. See the equation below.
(Eq 3) $ν=\frac{-ε_t}{ε_l}$