As the flow over an immersed object, such as a flat plate, has a laminar flow the analytical methods compare well to experimental results. However, as the flow starts to transition to turbulent flow, these analytical methods can no longer be relied on for accurate answers.
Transition from Laminar to Turbulent
A flow does become turbulent from laminar instantaneously. Instead there will be a transition from laminar to turbulent. This transition is dependent on the Reynolds number. For a flat plate the Reynolds Number is based off the distance from the leading edge of the flat plate, $Re_x=Ux/ν$. As a result, as a flat plates length increases it will start to transition into a turbulent flow. This transition will occur at Reynolds number, $Re_{xcr}$, between $2×10^5$ to $3×10^6$.
For a flat plate the transition from laminar flow to turbulent flow will not occur at a single location. Instead it will occur over a region of the plate’s length. Because of this, the transition will begin at random location on the plate where the Reynolds number is in the vicinity of $Re_x=R_e{xcr}$. This will continue to occur until the entire width of the flat plate is experiencing turbulent flow.
Transition form laminar to turbulent flow occurs because of instabilities in the flow field. These instabilities are caused by wide variety of variables. Some of these variables are surface roughness or a wiggle in the fluid flow as it flows over the plate. Depending on how these disturbance are introduced to the flow, they will either amplify other instabilities, or cancel out other instabilities stabilizing the flow. Generally, if the disturbance occurs in an area where $Re_x<Re_{xcr}$ the instabilities will stabilize causing the flow to return to a laminar state. However, in areas where $Re_x>Re_{xcr}$ the instability will grow causing turbulent flow.
Finally, as a flow transition from laminar to turbulent there will be a noticeable change in the shape of the boundary layer. As the flow enters a turbulent state the turbulent profile will be flatter and have a larger velocity gradient at the wall. In turn this will create a larger boundary layer thickness.
Turbulent Boundary Layer
Once a the fluid becomes turbulent, the flow profile will become very complex, random, and irregular. Basically the flow will be a jumbled mix of intertwined eddies. These eddies will be different sizes, and will have different angular velocities.
Due to the randomness of the flow there will be a considerable amount of mixing. However, despite this there will be a negligible amount of mass transferred over the boundary layer. On the other hand, there will be a considerable net transfer of x-component momentum perpendicular to the plate. In addition, particles that move away from the plate will gain y-component momentum from the fluid. Hence, the plate is acting as a momentum sink that is continuously extracting momentum from the fluid.
Due to the fact that there is no precise expression for shear stress, there is no exact solution for a turbulent boundary layer flow. However, approximations can be made using numerical solutions. In addition, the momentum integral equation can be used to find an approximation of the turbulent boundary layer flow. However, to use the momentum integral equation you will need a reasonable approximation of the velocity profile.
Finally, if you know the surface roughness of the flat plate, as well as the Reynolds number of the flow, the chart below can be used to determine drag coefficient. This chart is not needed for laminar flow since surface roughness is not important for laminar flow.
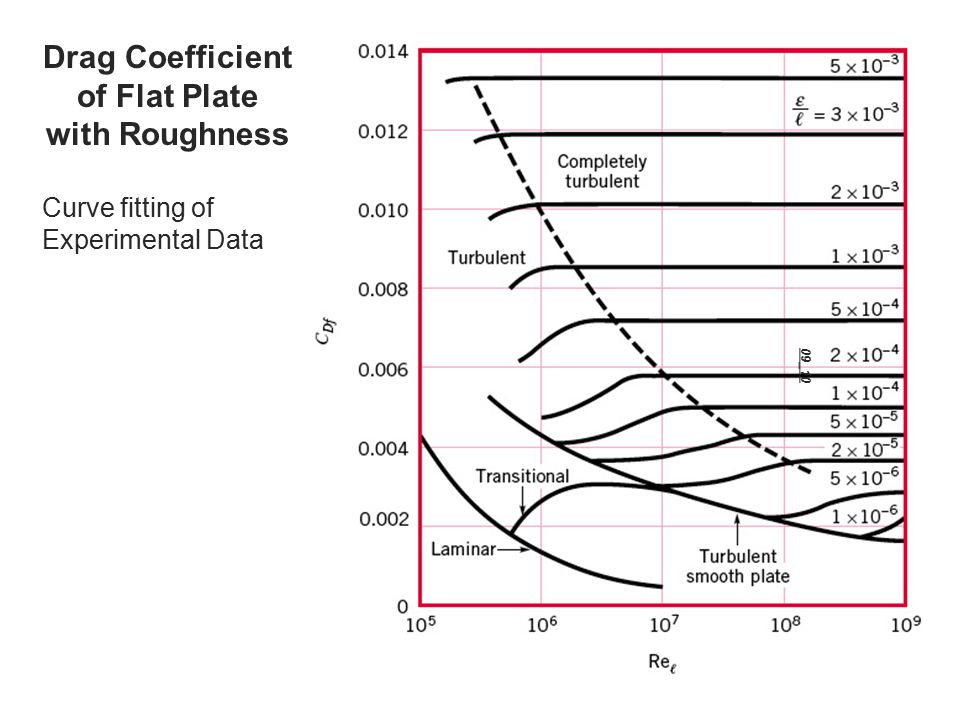
Image Reference: White F.M., Fluid Mechanics, 6th Ed., McGraw-Hill, New York, 2008