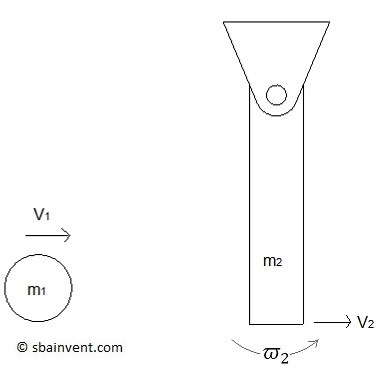
In a previous article I talked about central and oblique impacts on a particle. In addition to these types of impacts, an eccentric impact could occur. An eccentric impact will occur when the line connecting the center of mass of two rigid bodies does not coincide with the line of impact. Eccentric impacts will also occur if one or both of the bodies are constrained so that they will rotate around a fixed axis. Finally, an eccentric impact will effect the angular velocity of the two bodies.
Momentum and the Coefficient of Restitution
An impact will cause the momentum of one body to transfer to the other. Assuming that there are no external forces or moments acting on the bodies, than conservation of momentum can be used.
(Eq 1) $m_1(v_1) = m_2(v_2)$
linear conservation of momentum
(Eq 2) $I_1(ϖ_1) = I_2(ϖ_2)$
angular conservation of momentum
Equations 1 and 2 represent the general forms of conservation of momentum between two objects. However, the above equations do not consider what happens during an impact. When two objects come in contact with each other there will be a deformation impulse as well as a restitution impulse. The deformation impulse (P) will cause the objects two deform when the come in contact with each other. On the other hand the restitution impulse (R) will occur when the two object return to their original shape after the impact has occurred.

(Eq 3) $I_o(ϖ_B)_1 +r∫Pdt = I_oϖ$
(Eq 4) $I_oϖ +r∫Rdt = I_o(ϖ_B)_2$
$I_o$ = mass moment of inertia around the axis of rotation
$r$ = distance the impact is from the axis of rotation
$(ϖ_B)_1$ = initial angular velocity
$(ω_B)_2$ = final angular velocity
Equations 3 and 4 represent how the deformation and restitution impulse would affect the angular momentum of a rigid body rotating around a fixed axis.
Finally, the coefficient of restitution represents how elastic the impact is. There are two extremes that could occur. First, the coefficient of restitution could equal 1. When this is the case the impact is perfectly elastic. On the other hand a coefficient of restitution will cause the two bodies to stick together after the impact creating one body. Determining the ration of the deformation and restitution impulse will result in the coefficient of restitution.
(Eq 5) $e=\frac {∫Rdt} {∫Pdt}=\frac {r(ϖ_B)_2-rϖ} {rϖ-r(ϖ_B)_1} = \frac {v_B)_2-v} {v-(v_B)_1}$
or
(Eq 6) $ e = \frac{(v_B)_2-(v_A)_2}{(v_A)_1 – (v_B)_1}$
After two bodies impact each other you will have to determine the resulting velocity of both object. As a result you will need use a combination of conservation of momentum, energy equations, kinematics, and the coefficient of restitution.
Example
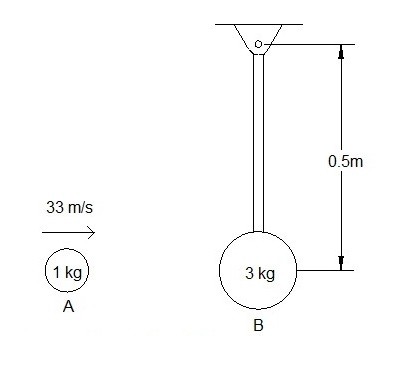
A ball with a mass of 1 kg strikes a ball hanging from a rope that has a mass of 3 kg. The 1 kg ball is initially travelling at 33$\frac{m}{s}$ while the 3 kg ball is at rest. Determine the angular velocity of the 3 kg ball after impact. Assume that rope will is always under tension. The coefficient of restitution is 0.6.
Solution
Step 1: Using conservation of momentum determine how the two bodies relate to each other.
$m_A(v_A)_1(r)+I_B(ϖ_B)_1) = m_A(v_A)(r)+m_B(v_B)_2(r)+I_B(ϖ_B)_2$
where
$m_A=1~kg$
$r$ = 0.5~m$
$(v_A)_1 = 33\frac{m}{s}$
$(ϖ_B)_1 = 0$
$I=3~kg(0.5m~m)^2 = 0.75~kg·m^2$
$(v_B)_2=0.5(ϖ_B)_2$
$16.5 = 0.5(v_A)_2 + 3.75(ϖ_B)_2$
Step 2: Using the coefficient of restitution solve for $(v_A)_2$ and $(ϖ_B)_2$.
$e=\frac{(v_B)_2-(v_A)_2}{(v_A)_1-(v_B)_1}$$=\frac{0.5(ϖ_B)_2-(v_A)_2}{33-0}=0.6$
$(ϖ_B)_2 = 6.6\frac{rad}{s},~CCW$
$(v_B)_2 = -16.5 \frac{m}{s}$