Impacts

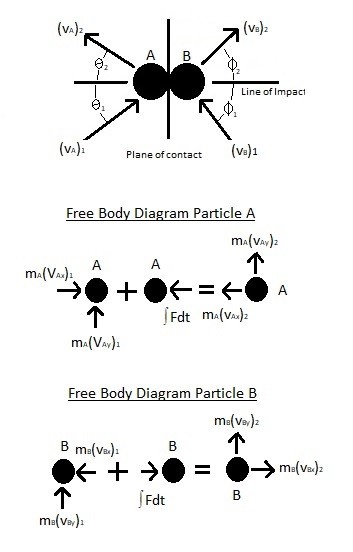
When two particle come in contact with each other an impact will occur.  The resulting impulse will determine how large the resulting force is. An example of an impact would be when you are hammering a nail, or when a baseball player hits a baseball when he is up to bat.  There are two types of impacts that a particle can experience, central and oblique.  A central impact occurs when when the center of mass of the two particles is in line with each other during contact.  In contrast when two particle hit each other at an angle an oblique impact will occur.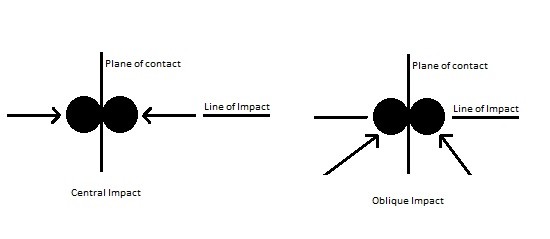

Mechanics of an Impact

As seen in the image below, before an impact the particle will moving towards each other at a certain velocity.  This velocity could be the same or it could be different.  There could also be cases where the particles are moving in the same direction, but the particle behind the particle in front would be moving faster which eventually will result in contact.  Once the impact occurs an impulse will result.  The particle will first deform. This deformation will cause an opposite but equal deformation impulse ∫P dt.  Once maximum deformation occurs the particle will at that instant be moving at the same relative velocity until they start to move away from each other.  Assuming there is no permanent deformation to either particle, as the particles move away from each other they will return to their original shape resulting in a restitution impulse ∫R dt.  After the impact has concluded the velocity and direction of the particles will change, as represented by the equation below.

(Eq 1)  $e=\frac{∫Rdt}{∫Pdt}=\frac{(v_B)_2-(v_A)_2}{(v_A)_1-(v_B)_1}$

(v_A)₁ = initial velocity of particle A

(v_A)₂ = final velocity of particle A

(v_B)₁ = initial velocity of particle B

(v_B)₂ = final velocity of particle B

e = coefficient of restitution

Coefficient of Restitution

Notice in the equation above there is a variable e called the coefficient of restitution.   The coefficient of restitution is the ratio of the relative velocity of the two particle after impact and the relative velocity of the two particle before impact.  If the collision between the two particle is perfectly elastic than e would equal 1.  On the other hand if the impact was completely plastic than e would equal 0.  Both these cases are theoretical.  Instead the coefficient of restitution is always a value between 0 and 1.

Example

Find the velocity of the two particle after impact occurs.

 

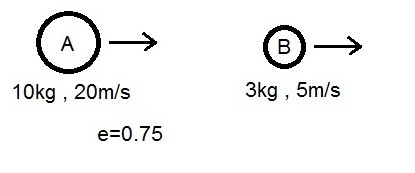
Solution

Step 1: Use equation 1.

$0.75=\frac{(v_B)_2-(v_A)_2}{20-5}$

$11.25 = (v_B)_2-(v_A)_2$

Step 2: The conservation of momentum equation will need to be used to solve for the two unknown variables.

$m_B(v_B)_1+m_A(v_A)_1=m_B(v_B)_2+m_A(v_A)_2$

$3~kg(5~m/s)10~kg(20~m/s)=3~kg(v_B)_2+10~kg(v_A)_2$

$215 = 3~kg(v_B)_2+10~kg(v_A)_2$

Step 3:  Solve for $v_A$ and $v_B$.

$v_A=13.9~m/s$   $v_B=25.2~m/s$

Oblique Impact

So far I have only talked about central impacts.  However, as mentioned above, there can also be cases where there are oblique impacts.  For central impacts we can intuitively determine the direction of particle after impact, and we only have to determine the change in velocity.  This will result in two unknowns $(v_A)_2$ and $(v_B)_2$.  While on the other hand an oblique impact will have four unknowns due the angle of contact.  If the initial velocity and angle of impact are known, than the four unknowns would be as follows $(v_A)_2$, $(v_B)_2$, $θ_2$, and Φ_2.  You will need to use vector algebra to find the unknowns.

 

Previous  |  Next

⇑  |  ⇓