Energy has two basic forms, work and heat. Work is energy that is used to perform a mechanical task, which for dynamics, can be broken down into two different forms, Potential & Kinetic Energy. Heat on the other hand is energy that is lost do to inefficiency in a system. In a system there will always be energy that is converted into heat, due to the laws of Thermodynamics.
Potential Energy
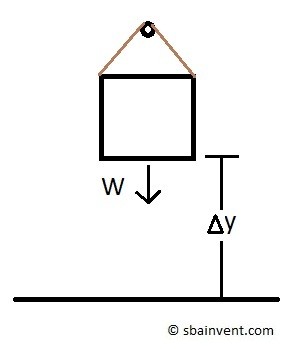
One form of work is potential energy or stored energy which can later be converted to motion. For example, what if you had a rigid body suspended in the air? If you were to remove the support holding that box, it would fall. Falling is a form of motion. This means that the product of the weight of the rigid body and the height it is off the ground will equal the total potential energy of the rigid body.
(Eq 1) $U_W=-WΔy$
$W$ = Weight
$Δy$ = objects height
$U_W$ = Potential energy of hanging mass
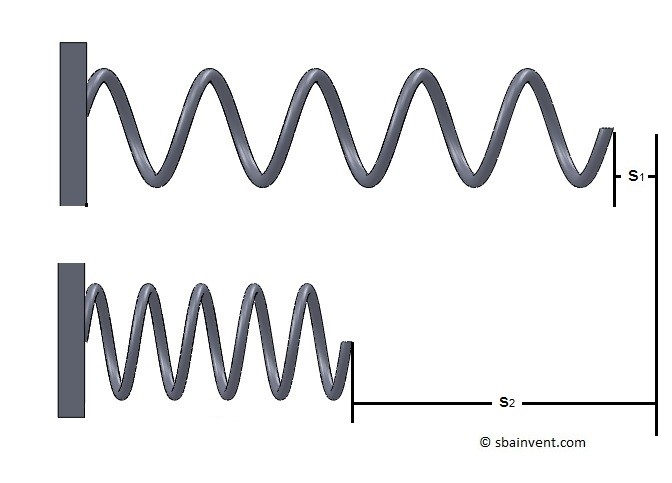
Now what if you stretch, compress, or torqued a spring? Once you released the spring it will want to return to its original state of rest. However, the spring will need energy to return to its original state of rest. The stored energy in the spring is potential energy. Now to calculate the total stored energy in a spring you will need to first determine the spring constant and than determine how much the spring has deflected.
(Eq 2) $U_s=\frac{1}{2}kΔs^2$
$k$ = spring constant
$Δs$ = spring deflection
$U_s$ = Potential energy of a spring
Kinetic Energy
Kinetic energy on the other hand represents the energy of motion. When a particle or a rigid body is moving at a certain velocity it will have certain amount of kinetic energy that is dependent on the mass and velocity of the particle or rigid body. In order to stop that particle or rigid body the kinetic energy will have to go to zero. When the kinetic energy goes to zero it will either be stored as potential energy or dissipate into heat.
(Eq 3) $T=\frac{1}{2}mv^2$
$m$ = mass
$v$ = velocity
Equation 3 represents a rigid body or particle that has translational velocity. However, in addition to translation motion, a rigid body can also rotate around an axis, which a particle cannot. To find the to kinetic energy of angular velocity you would need to use the equation below.
(Eq 4) $T=\frac{1}{2}Iϖ^2$
$I$ = Mass Moment of Inertia
$ϖ$ = angular velocity