The laws of conservation of energy state that it is impossible to create energy as well as destroy it. Instead energy can only transfer from one form to another form of energy. There can be many different energy forms that energy can take the form of. However, for dynamics, the main type of energy that are of focus are kinetic energy, potential energy, and energy transferred by a moment or a force.
Conservation of Energy: Forces and Moments
As a force or a moment acts on a rigid body that rigid body will have to restrain that force. If the rigid body isn’t constrained, the force or moment will cause the rigid body to move. When a force is acting on the body the transnational velocity will increase or decrease depending on the direction of the force and the original velocity. On the other hand a moment will increase or decrease the rigid body’s angular velocity. When the velocity increases due to a force or moment the kinetic energy increases. On the other hand if the force or moment cause the rigid body’s velocity to decrease the kinetic energy will decrease. The equation below is the conservation of energy motion that will relate kinetic energy to a force or a moment.
(Eq 1) $T_1 +\sum{}U_{1-2}=T_2$
$T_1$ = Initial Kinetic Energy
$T_2$ = Final Kinetic Energy
$U_{1-2}$ = Energy input from force and moment
Conservation of Energy: Potential & Kinetic Energy
In addition to a force or a moment causing a change in kinetic energy. Potential energy will also have the capability to cause a change in kinetic energy. This is because potential energy is a stored energy value that will create motion when it is released.
(Eq 2) $T_1+V_1=T_2+V_2$
$V_1$ = Initial Potential Energy
$V_2$ = Final Potential Energy
Example
A wheel with a mass of 10 kg has a spring with a spring stiffness of 60 $\frac{N}{m}$ attached to it. A moment of 6 N-m is applied to the wheel. Determine the angular velocity of the wheel after its center moves 0.13 m. The wheel is initially at rest and will not slip.
Solution
First create a free body diagram of all of the forces.
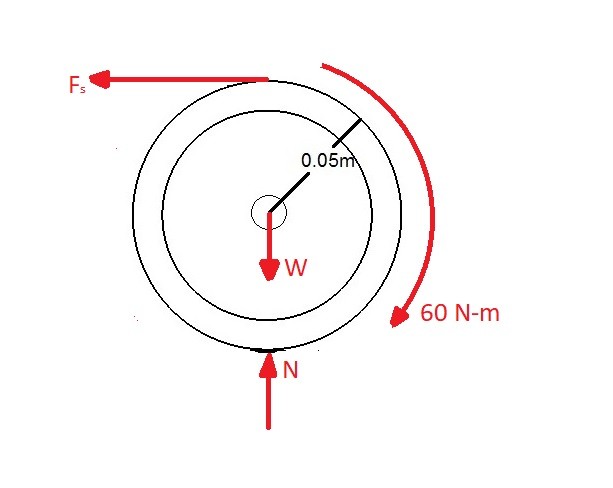
To solve this problem you would use equation 1.
$T_1 +\sum{}U_{1-2}=T_2$
In the above equation since wheel is initially at rest there will be no initial kinetic energy.
$T_1$ = 0
Next, the energy $U_{1-2}$ will be calculated by two contradicting moments, the moment 60$\frac{N}{m}$ and the moment caused by the spring force as the wheel moves away from its initial position of rest.
$U_{1-2}=Mθ-\frac{1}{2}ks^2$
$θ=\frac{0.13}{.05}=2.16~rad,~s=2(0.05~m)(2.6~rad)=0.26~m$
$U_{1-2} = 6(2.6)-\frac{1}{2}(60)(0.26)^2=13.6~J$
Finally, determine the angular velocity of the wheel.
$13.6~J=\frac{1}{2}mv^2+\frac{1}{2}Iϖ^2$
$I=\frac{1}{2}mr^2=0.013~kg·m^2,~v=0.05mϖ$
$ϖ=26.8\frac{rad}{s}$