When studying thermodynamics the processes that are talked about are almost always reversible processes. The definition of a reversible process is a process that can be reversed without leaving traces of the process on the surroundings. In other words the process can always be returned to its initial state. Reversible processes do not occur in nature, but instead are ideal processes. The opposite of a reversible process is an irreversible process. Any process that cannot return to it original state is an irreversible process. Irreversible processes are real processes.
So why do engineers focus on reversible processes instead of irreversible processes? They do this because a reversible process is much easier to analyze. An irreversible process can have unknowns that can’ t be accounted for. Also, if you solve the reversible process, which is an ideal process. You can use those results and compare them to the results from an actual process that has been measured. Basically the reversible process is a theoretical limit for its corresponding irreversible process. If your irreversible process provides better results than your reversible process, then you either calculated your reversible process wrong, or something is wrong with your measurements.
So what causes a process to have irreversibility’s? Well first most reversible processes assume that a process is quasistatic. In real life, however, it’s not practical for a process to happen slow enough to be quasistatic. This in turn results in unrestrained expansion, which can actually cause a pressure difference within the cylinder that the gas is expanding, or be compressed in. Another common irreversibility is friction. Friction causes heat, which is lost energy from the system that cannot be reversed. Heat transfer can also cause irreversibility. An example is a hot liquid that cools in air, the heat will not readily go back into that liquid, so the process cannot be reversed. Finally, another example of an irreversibility is an inelastic deformation. If something has be permanently deformed it will not release the same amount of energy that was used to deform it.
Carnot Cycle
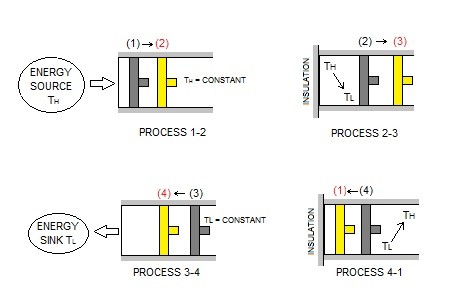
The Carnot Cycle is one of the most widely used ideal and reversible cycles. It is stated that nothing in real life can be more efficient then the Carnot Cycle. Basically the Carnot Cycle is a theoretical heat engine that has two Isothermal processes and two adiabatic processes. It is typically represented by a piston that is in a quasistatic state where the gas inside is expanded by a heat source, and then a heat sink is used to slowly remove the heat from the piston. Refer to image below.
“A heat engine cannot operate by exchanging heat with a single reservoir source and a refrigerator cannot operate without net energy input from an external source.”
1. The efficiency of any irreversible heat engine is always less than the efficiency of the reversible cycle that represents that heat engine.
2. The efficiency of all reversible heat engines operating between the same two reservoirs are the same.
Carnot Heat Engine
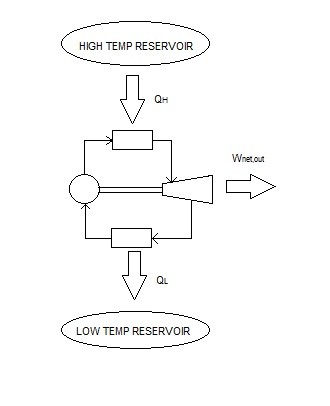
Like with any heat engine, the Carnot Heat Engine must operate between two reservoirs, where one reservoir provides energy and the other removes excess energy. Just like all heat engines that Carnot Heat Engine cannot be 100% efficient, otherwise the second law of thermodynamics would be violated. The Carnot Heat Engine, however, will tell the engineer the highest possible efficiency that any heat engine could theoretically obtain if it were operate between those two reservoirs. Refer to the equation below to calculate the efficiency of a Carnot Heat Engine.
(Eq 1) $ η_{th} = 1-\frac{Q_L}{Q_H}=1-\frac{T_L}{T_H}$
Carnot Refrigerator & Heat Pumps
By using a reverse Carnot Cycle it is possible to determine a theoretical COP for a refrigerator or heat pump in relation to the Carnot Cycle. Refer to the equations below.
(Eq 2) $COP_R=\frac{1}{\frac{Q_H}{Q_L}-1}=\frac{1}{\frac{T_H}{T_L}-1}$
(Eq 3) $COP_{HP}=\frac{1}{1-\frac{Q_L}{Q_H}}=\frac{1}{1-\frac{T_L}{T_H}}$
Perpetual Motion Machine
A perpetual motion machine is a machine that has a thermodynamic process that violates either the first or the second law of thermodynamics. Devices that violate the 1st law are called perpetual motion machines of the 1st class. An example, of a perpetual motion machine of the first class would be a device that has an energy output greater than its energy input. By the conservation of energy input must equal energy output. Devices that violate the 2nd law are called perpetual motion machines of the 2nd class. For example if it is claimed that a device has an efficiency that is greater than the Carnot Cycle or can operate on only one heat reservoir then it would be considered a perpetual motion machine. As of the year 1918 the U.S. patent department will no longer consider perpetual motion machine applications.