There are two types of systems; open and closed. In this section I am going to be discussing the mass and energy analysis of an open system.
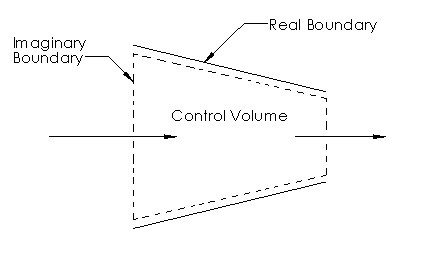
First, however, let’s briefly go over what an open system is. An open system is a region in space that has been selected to study. It’s boundary is defined by a control volume. The control volume can consist of both real and imaginary boundaries. Due to the fact that a system is open, mass can flow through the system. In turn, energy can enter or leave the system as mass is flowing through the system. The image below represents the control volume of a nozzle.
Conservation of Mass and Conservation of Energy
To perform a mass and energy analysis you will need to have an understanding of what conservation of mass is. Conservation of mass happens to be one of the fundamental principles of nature. Basically, like energy, mass cannot be created or destroyed during a process. However, as shown by Einstein mass and energy can be converted to each other.
(Eq 1) $E=mc^2$
$E$ = energy
$m$ = mass
$c$ = speed of light $2.9979×10^8$
As a result, from this equation it can be concluded that when the mass of a system changes the energy of the system will also change. However, generally the change in mass is extremely small, with a nuclear reaction being the exception.
Mass Flow
Mass flow represents the amount of mass flowing through a cross-section per unit time. It is denoted by $\dot{m}$. The following equation represents the differential mass flow rate across a small area element.
(Eq 2) $δ\dot{m}=ρv_n~dA_c$
$ρ$ = fluid density
$v_n$ = normal velocity
$dA_c$= area element
To obtain the mass flow rate through the entire cross-sectional area, such as that of a pipe, equation 2 will be need to be integrated. In turn, this will result in the following equation.
(Eq 3) $\dot{m}=\int{_{A_c}}~δ\dot{m}=\int{_{A_c}}~ρv_n~dA_c$ (kg/s)
Equation 3 will always provide the exact value for mass flow. However, due to the integration, this is not always practical. Instead it is more convenient to present mass flow using average values over the cross-sectional area. For example, for compressible flows, both density and the normal velocity can vary across the cross-sectional area. However, for most practical applications density is essentially uniform. On the other hand velocity will always vary across the cross-section. The velocity will be zero where it contacts a wall. While for a pipe the velocity will be at its maximum on the center-line of the pipe.
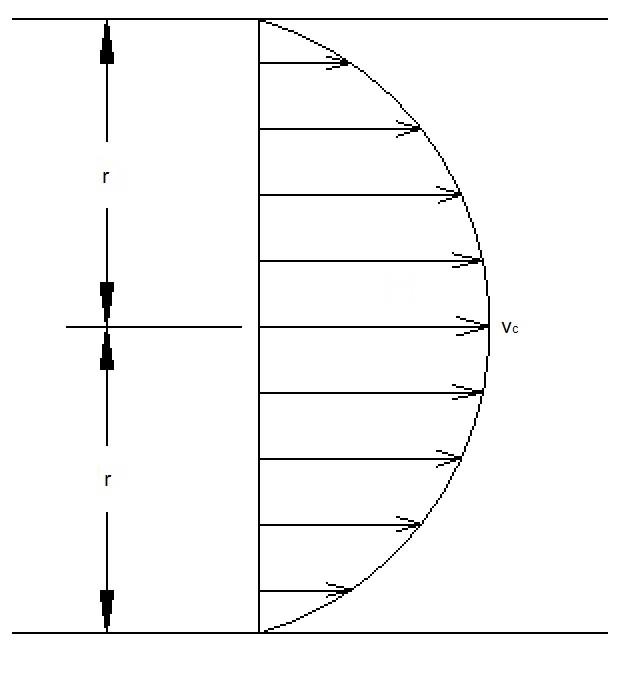Even though the velocity changes across the cross-section, the velocity can be defined as an average velocity. To define the average velocity the following equation would be used.
(Eq 4) $v_{avg}=\frac{1}{A_c}\int{_{A_c}}~V_n~dA_c$
Finally, for an incompressible flow, and some compressible flows, equation 3 can be simplified to the following.
(Eq 5) $\dot{m}=ρv_{avg}A_c$ (kg/s)
If the flow is compressible than the density will represent the bulk average density across over the cross-section.
Conservation of Mass
For a control volume the conservation of mass is expressed by the following statement. “The net mass transfer to or from a control volume during a time interval is equal to the net change in total mass within the control volume during $Δt$.” In other words,
(Eq 6) $m_{in}-m_{out}=Δm_{CV}$
Equation 6 can also be expressed in rate form.
(Eq 7) $\dot{m}_{in}-\dot{m}_{out}=dm_{CV}/dt$
Next, the conservation of mass relation for a fixed control volume is expressed using the following.
(Eq 8) $\frac{d}{dt}\int{_{CV}}ρdV+\int{_{CS}}ρ(\overrightarrow{v}·\overrightarrow{n})~dA=0$
This equation states that the time rate of change of mass in the control volume plus the net flow rate through the control surface will equal zero.
Steady Flow Processes
For a steady-flow process to occur the total amount of mass within the system cannot change with time. In other words, $m_{CV}=constant$. In order for this to occur in an open system the mass entering the control volume must be the same as the mass exiting the system.
As a result,
(Eq 9) $\sum_{in}\dot{m}=\sum_{out}\dot{m}$
For a single stream steady-flow system, like a nozzle, equation 9 is simply the following.
(Eq 10) $\dot{m}_1=\dot{m}_2$ → $ρ_1v_1A_1=ρ_2v_2A_2$
Flow Work
When you are analyzing a control volume you will need to consider mass flow across the boundaries. More specifically you will need to be aware of the work is required to push the mass into or out of the control volume. In turn, you will be determining the flow work that is necessary to maintain continuous flow. This can be determined by using the following equation.
(Eq 11) $w_{flow}=Pν$
$ν$ = specific volume
$P$ = fluid pressure
This equation is valid whether the fluid is being pushed into or out of the control volume.
Total Fluid Energy
The energy of a compressible system is made up of three parts. These parts are the internal, kinetic, and potential energies. In turn, this is expressed as the following.
(Eq 12) $e=u+ke+pe=u+\frac{v^2}{2}+gz$ (kJ/kg)
$u$ = internal energy
$g$ = gravitational constant
$z$ = elevation of the system in respect to some external reference point.
$v$ = fluid velocity
However, in order to obtain the total energy of a fluid you must include the flow work of the fluid within this equation.
(Eq 13) $θ=Pν+e=Pν+(u+ke+pe)$ (kJ/kg)
Finally, since $Pν+u$ is defined as enthalpy, $h$, than equation 13 will become the following.
(Eq 14) $θ=h+ke+pe=h+\frac{v^2}{2}+gz$ (kJ/kg)
By using enthalpy to determine the total fluid energy you will not need to be concerned about the flow work since it will considered by enthalpy.
Mass Energy Transport
In equation 14, $θ$ represents the total energy per unit mass. As a result, the total energy of a flowing fluid of mass $m$ is simply $mθ$. In addition, the rate of energy flow can be determined from the mass flow by simply using $\dot{m}θ$.
(Eq 15) $E_mass=mθ=m\left(h+\frac{v^2}{2}+gz\right)$ (kJ)
(Eq 16) $\dot{E}_mass=\dot{m}θ=\dot{m}\left(h+\frac{v^2}{2}+gz\right)$ (kW)
Finally, since the mass flow across an inlet or an outlet can change with time to analyze the total energy transported by mass a general equation will need to be used. This general equation is represented in the equation below.
(Eq 17) $E_{in,~mass}=\int{_{m_i}}θ_iδm_i=\int{_{m_i}}\left(h_i+\frac{v^2_i}{2}+gz_i\right)δm_i$
