Entropy is the measurement of molecular disorder within a system. As the temperature of the system increases the entropy will increase, and as it cools the entropy will decrease. This means that a solid will have lower entropy then a gas would. Due this fact the third law of thermodynamics can be defined. “Entropy of a pure crystalline substance at absolute zero temperature is zero.”
When people think of thermodynamics, entropy does not normally come to mind. However, entropy is a very important property to consider, since it is the opposite of work. Work can be defined as organized energy, with a known direction and quantity. Entropy on the other hand is chaos, and even though individual particle can have a predefined quantity and direction of energy, this will be canceled out by the randomness of other particles within the system. For example, wind blowing through a windmill is organized energy creating work. On the other hand air inside the room you are sitting in has energetic particles colliding into you right now. However, they are colliding into you at all directions in a chaotic manner, so that their energy is canceled out and you don’t notice their presents, which is entropy.
During a thermodynamic process the total entropy of the system can either remain constant, or it will increase. If the process is a reversible process then the entropy of the system will remain constant. However, the entropy will increase if the process is irreversible. Due to this fact the entropy change cannot be negative without violating the second law of thermodynamics. This is a major concern for engineers, because an increase in entropy can prematurely end chemical reactions and other thermodynamic processes. Due to this fact it is speculated that as the entropy of the universe continues to increase it will eventually reach a point that all thermodynamic processes will stop.
Entropy can also sometimes be referred to as the Clausius Inequality, which was first stated by German physicist R. J. E. Clausius and is represented by the equation below.
(Eq 1) $\oint{\frac{δQ}{T}}≤0$
Notice that the cyclic integral above states that the change in heat over temperature cannot be greater than zero. If it equals zero then the cycle is reversible, and there is no change in the heat energy being released. However, for an irreversible process the irreversibilities will cause an increase in heat energy causing the change in heat to be negative. This means that if the overall entropy increases then more energy will be converted to heat that cannot be recovered instead of being successfully used as work.
T-s Diagrams
T-s diagrams are used to show how a change in entropy can affect the temperature of a pure substance when that substance is kept at a constant pressure or specific volume. If a T-s diagram is used to represent the process, the area under the curve will represent the heat transfer that took place during the process.

(Eq 2) $s=s_f+xs_{fg}$
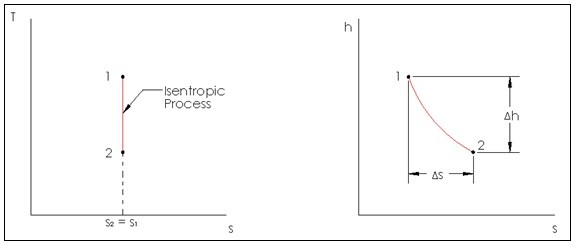
Isentropic Process
A process that does not have a change in entropy is an isentropic process. Though very similar to a reversible adiabatic process, an isentropic process is not necessarily reversibly adiabatic, but a reversibly adiabatic process is always isentropic.
In real life there are no processes that are truly isentropic or adiabatic, since those two processes are ideal processes. However, there are some engineering devices that can be considered essentially adiabatic. They are pumps, turbines, nozzles, and diffusers to name a few. So when studying these devices an isentropic model can be used. Below is an image of an isentropic process on a T-s diagram, and an adiabatic process on an h-s diagram for a steady flow device.
Entropy Change of Solids, Liquids, and an Ideal Gas
For an accurate prediction of entropy change the thermal dynamic tables should be used. However, in certain cases reasonable assumptions can be made to calculate the entropy change.
To predict entropy without use of the thermal dynamics tables to general equations could be used. Refer to equations 3 and 4. Both equations can only consider an isothermal process. If the process is not isothermal a more complex equation will need to be derived to relate the change in temperature to δQ.
(Eq 3) $ds = \frac{du}{T}+P\frac{dv}{T},~where~du=c_vdT$
(Eq 4) $ds=\frac{dh}{T}-P\frac{dv}{T},~where~dh=c_pdT$
Notice in both equations 3 and 4 the specific heat for volume can be used to estimate the specific energy, while the specific heat for pressure can be used to estimate the change in enthalpy. This can only be used for ideal gases, and is more accurate for small temperature changes or linear specific heat relation to temperatures so that an average can be used. If this relationship is not linear, large changes in temperature will affect the accuracy of the calculation.
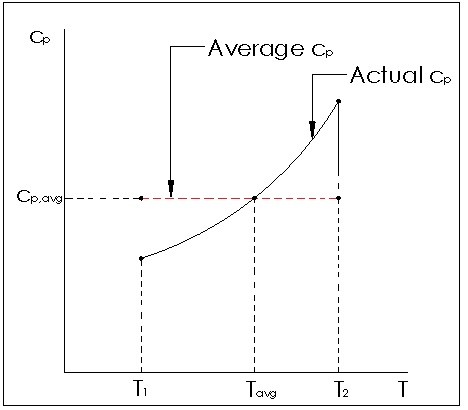
(Eq 5) $ds=\frac{du}{T}=c\frac{dT}{T}$
Finally, for an gas going under an isothermal process equations 3 and 4 can be modified to include the ideal gas law. Refer to equations 6 and 7.
(Eq 6) $ds=c_{v_{avg}}·ln\frac{T_2}{T_1}+R·ln\frac{V_2}{V_1}$
(Eq 7) $ds=c_{p_{avg}}·ln\frac{T_2}{T_1}+R·ln\frac{P_2}{P_1}$
For an ideal gas that is going under an isentropic process the temperature, specific volume, and pressure can be related using the following equations. These equations assume constant specific heat which means they will lose accuracy as the temperature difference increases.
(Eq 8) $\left(\frac{T_2}{T_1}\right)_{s=const.}=\left(\frac{v_1}{v_2}\right)^{k-1}$
(Eq 9) $\left(\frac{T_2}{T_1}\right)_{s=const.}=\left(\frac{P_2}{P_1}\right)^{(k-1)/k}$
(Eq 10) $\left(\frac{P_2}{P_1}\right)_{s=const.}=\left(\frac{v_1}{v_2}\right)^{k}$