A closed system is a system that has a fixed amount of mass. This mass cannot cross the boundary of the system. As a result, the mass cannot leave or enter the system.
There are two types of closed systems. The first type has a fixed boundary. On the other hand, the second type has a moving boundary. Whatever the case, as long as mass does not enter or leave the system, it is considered a closed system.
Below is an example of a closed system with a moving boundary.
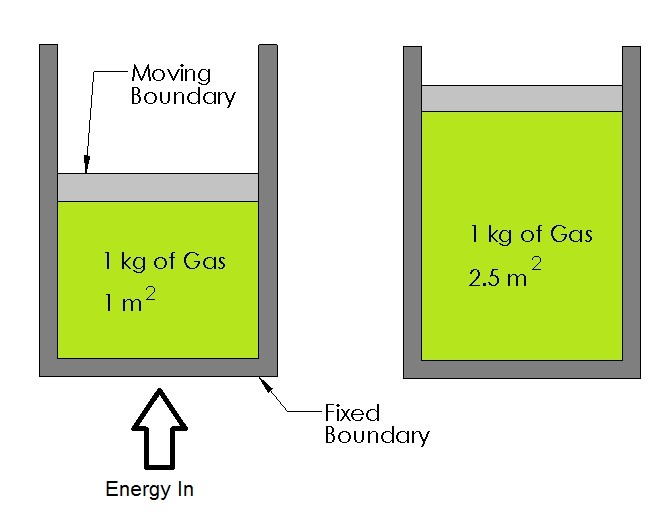
In this example there is a cylinder that is filled with gas. As the gas expands it will move one of the walls of the cylinder. However, the mass of the gas inside the cylinder will remain the same since it cannot cross the boundary of the system.
Unlike mass, energy is allowed to cross the boundary of the system. However, there is a special case when energy will not cross the boundary. This is known as an isolated system.
Moving Boundary Work of a Closed System
One form of work is the expansion or compression of gas inside a cylinder. In order for the process to occur one of the inner faces of the piston will have the ability to move back and forth. The moving face represents a moving boundary layer. In turn, the resulting work is called moving boundary work, which can be simply called boundary work.
Moving boundary work is the primary form of work inside an automobile engine. However, since the process inside an automobile occurs so fast, thermodynamic analysis alone cannot analyze the process. The reason for this is because the gas inside the cylinder never reaches equilibrium. As a result, the boundary work has to be determined through measurement.
Unlike a cylinder in a car engine, a quasi-equilibrium process can be analyzed by applying thermodynamic principles. This is because the substance remains nearly in equilibrium during the process. A quasi-equilibrium process can be used to approximate the process of a real engine. However, under identical conditions the approximation of the work output of the real engine will be at its maximum. In addition, if a compressor was be analyzed, a quasi-equilibrium process would represent the minimum work input.
Boundary Work on a Piston
To determine the work on a piston, you will need to look at the distance the piston traveled while in a quasi-equilibrium state. By doing this the differential work can be expressed using the following equation.
(Eq 1) $δW_b=F~ds=PA~ds=P~dV$
$P$ = initial pressure of the gas (absolute pressure)
$V$ = total volume
$A$ = cross-sectional area of the piston
$F$ = Force
$s$ = distance
In the above equation, the pressure is always absolute pressure. As a result, it will always be positive. However, the volume change $dV$ is positive during expansion and negative during compression. Hence the boundary work will be positive during expansion and negative during compression. Finally, the total boundary for the entire process is determined by adding all of the differential works from the initial to final state.
(Eq 2) $W_b=\int{}^2_1~P~dV$
The above equation is only used when there is a functional relationship between pressure and volume. In other words, $P=f(V)$. This equation represents the process path on the a $P-V$ diagram.
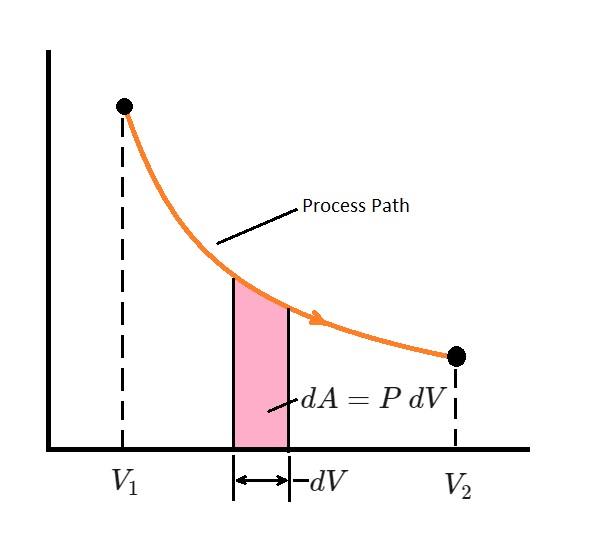
Finally, the total boundary work represents total area under the process curve. More specifically, “the area under the process curve on a $P-V$ diagram is equal, in magnitude, to the work done during a quasi-equilibrium expansion or compression process of a closed system.”
Work represent the mechanism of energy interaction between a system and its surrounding, where $W_b$ is the amount of energy transferred through expansion or contraction. As a result, the transferred energy will appear somewhere else. Since energy is conserved we will need to account for this transferred energy. Below is example of energy is accounted within a car engine.
(Eq 3) $W_b=W_{friction}+W_{atm}+W_{crank}=\int{}^2_1(F_{friction}+P_{atm}A+F_{crank})dx$
This equation represents work needed to overcome friction, the work required to push atmospheric air out of the way, and the work required to rotate the crankshaft.
Polytropic Process
A plolytropic process is used to represent the actual expansion and compression process of gases. It is represented by the equation below.
(Eq 4) $P=CV^{-n}$
In this equation both $C$ and $n$ are constants. After substituting this equation into equation 2 the following expression will result.
(Eq 5) $W_b=\int{}^2_1~P~dV$$=\int{}^2_1~CV^{-n}~dV$$=C\frac{V_2^{-n+1}-V_1^{-n+1}}{-n+1}$$=\frac{P_2V_2-P_1V_1}{1-n}$
where
$C=P_1V_1^n=P_2V_2^n$
For an ideal gas, $PV=mRT$, equation 5 can be rewritten as the following equation.
(Eq 6) $W_b=\frac{mR(T_2-T_1}{1-n}$
where
$n≠1$
If $n=1$, than the boundary work equation becomes the following.
(Eq 7) $W_b=\int{}_1^2~P~dV$$=\int{}^2_1~CV^{-1}~dV=PV~ln\frac{V_2}{V_1}$