It is very easy to convert work into other forms of energy such as heat. However, converting other forms of energy to work is not easy. For example think of a fan running in a room. As that fan is running, the work energy to run the fan will transfer into the internal energy of the air. In order for this energy to leave the air it will need to leave in the form of heat energy. This process cannot be reversed. As a result, heat cannot be converted directly into work. Instead a special devices called a heat engine has to be used to convert heat to work.
Heat Engine Characteristics
Heat engines can take on many different forms. As a result, they can be considerably different from one another. However, all of them will have the same characteristics.
- All heat engines receive heat from a high-temperature source.
- Part of the heat from the high-temperature source is converted to work usually through the use of a shaft.
- The remaining heat is rejected to a low temperature sink.
- All heat engines operate on a cycle.
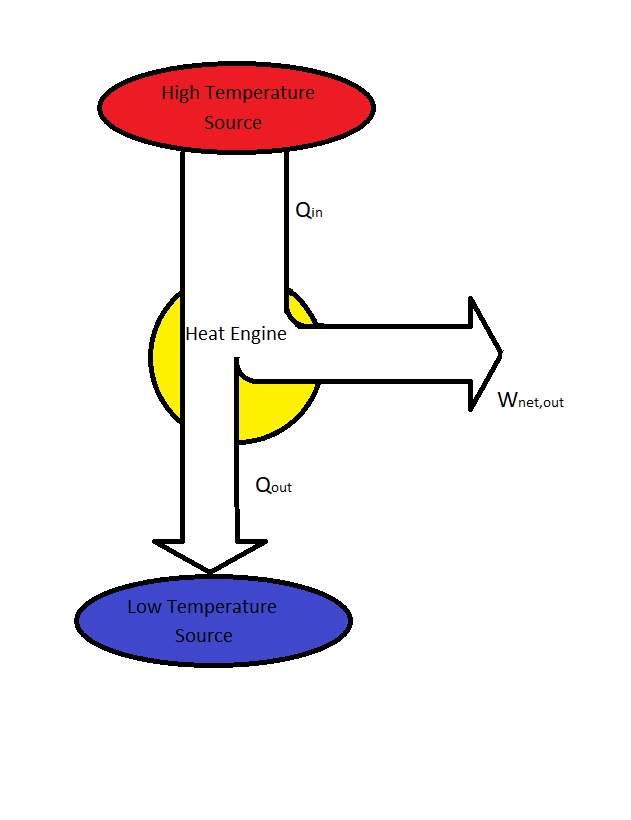
What is a Heat Engine?
Like most cyclic device heat engines use a working fluid which heat is transferred to and from. Heat engines do not include engines that involve internal combustion. These type of engines operate on a mechanical cycle not a thermodynamic cycle. The reason for this is because fluid inside an internal combustion engine does not undergo a complete cycle. This is because the exhaust is not cooled inside the engine but is instead purged and replaced with a fresh air-and-fuel mixture.
On the other hand, a steam power plant best represent the definition of a heat engine. A steam power plant is an external-combustion engine. This means that the combustion takes place outside the engine. As a result, thermal energy will be transferred to the steam as heat during the process. Below is simplified schematic of a a steam power plant.
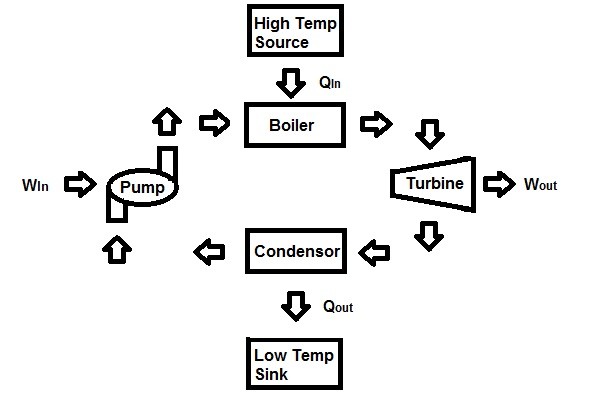
Where,
$Q_{in}$ = Heat supplied to the steam inside the boiler from a high temperature source. (Furnace)
$Q_{out}$ = Heat rejected from the steam inside a condenser to a low temperature sink. (Lake, Ocean, River, Atmosphere, etc.)
$W_{out}$ = work delivered by the steam from it expanding in the turbine.
$W_{in}$ = Work required to compress the water to boiler pressure.
To determine the net work output you would find the difference between the total work output and the total work input.
(Eq 1) $W_{net,out}=W_{out}-W_{in}$ (kJ)
In addition, the net work can also be determined solely from the heat transfer data. Hence,
(Eq 2) $W_{net,out}=Q_{in} – Q_{out}$
Thermal Efficiency
During a cycle $Q_{out}$ represents the magnitude of energy that was wasted to complete the cycle. For a cycle $Q_{out}$ can never be zero. In turn, this results in the net work output always being less than the heat input. Because of this only a fraction of the heat transferred to the heat engine is converted into work. How much of this heat is converted to work is dependent on thermal efficiency, $η_{th}$. For a heat engine, the following equation is used to calculate thermal efficiency.
(Eq 3) $η_{th}=\frac{W_{net,out}}{Q_{in}}$
Thermal efficiency can also be calculated using the following equation.
(Eq 4) $η_{th}=1-\frac{Q_{out}}{Q_{in}}$
Kelvin-Planck Statement
Kelvin-Planck statement is a statement of the second law of thermodynamics. It takes in consideration that no matter how efficient a cycle is there must be some rejected heat to a low temperature reservoir. The Kelvin-Planck statement is expressed as the following.
“It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work.”
This means that there is no heat engine that can have 100% efficiency.