In addition to circular piping, there is also noncircular piping. When noncircular pipes are used the same type of analysis that is used on round piping is used. However, the exact cross-sectional shape still needs to be taken in consideration.
Just like with circular piping, theoretical results for a laminar flow can be calculated for a noncircular pipe. However, this can become mathematically cumbersome. In order to determine the velocity profile, the following function will be used.
(Eq 1) $v=u(y,~z)\hat{i}$
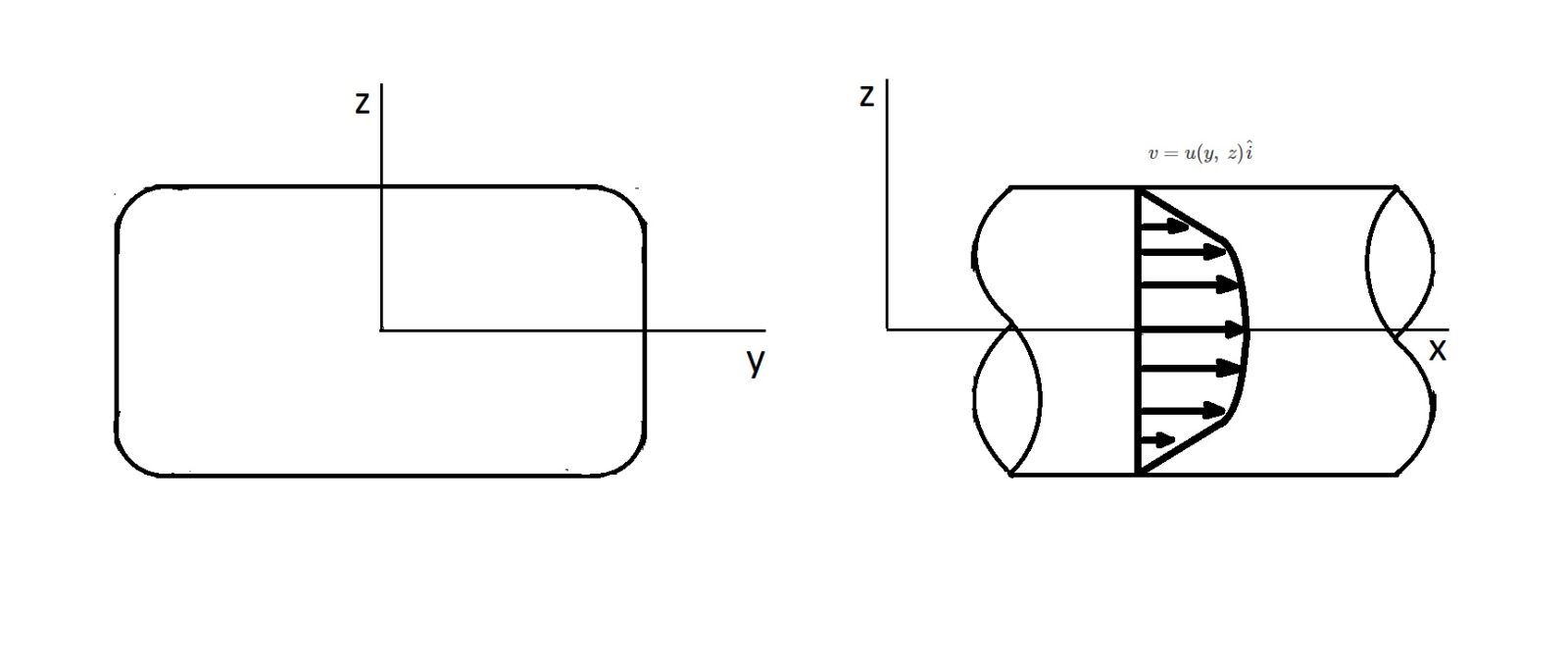
As a result, to determine the governing equation that will derive the velocity profile, a partial differential equation is needed. This equation is found by using Navier-Stokes Equations.
Hydraulic Diameter
On the other hand, there is a much simpler method than using a partial differential equation. Instead of using a partial differential equation, the hydraulic diameter can be used. To find the hydraulic diameter you will need to use the following equation.
(Eq 2) $D_h=\frac{4A}{P}$
$A$ = cross-sectional area
$P$ = the perimeter of the cross-sectional area.
This equation can be used for any cross-sectional shape to calculate the cross-sectional area. Finally, once the hydraulic diameter is known, it is used in the place of the diameter, $D$, that would otherwise be use for a circular pipe. For example, if you were to calculate the Reynolds number of a noncircular cross-section, you would modify the Reynolds number equation in the following manner.
For a circular pipe,
$Re=\frac{ρvD}{μ}$
For a noncircular pipe,
$Re_h=\frac{ρvD_h}{μ}$
Friction Factor for Laminar Flow, Noncircular Pipes
The data below will allow you to determine the friction factor for an annulus as wells as a rectangular cross-section.
Annulus
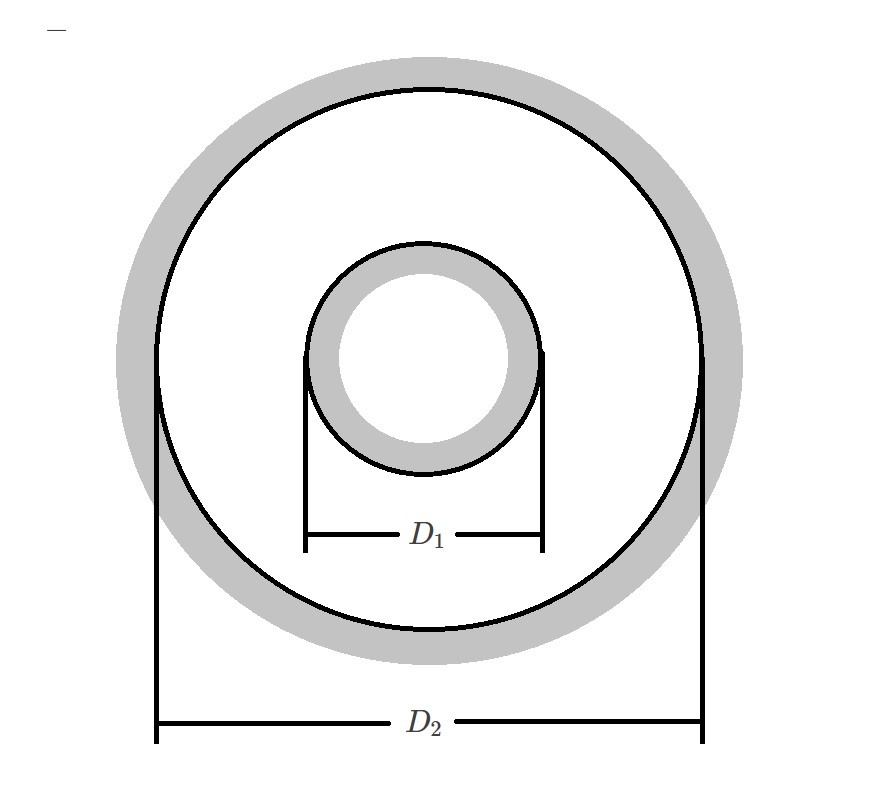
$D_h=D_2-D_1$
|
Parameter |
$C=fRe_h$ |
|
$D_1/D_2$ |
|
|
0.0001 |
71.8 |
|
0.01 |
80.1 |
|
0.1 |
89.4 |
|
0.6 |
95.6 |
|
1.00 |
96.0 |
Rectangle
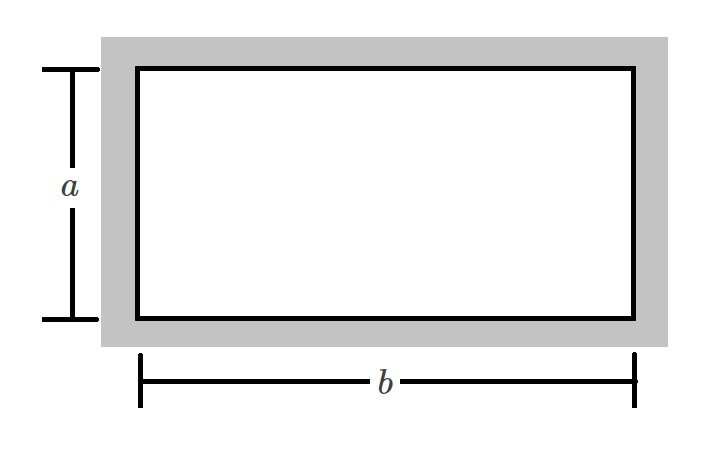
$D_h=\frac{2ab}{a+b}$
|
Parameter |
$C=fRe_h$ |
|
$a/b$ |
|
|
0 |
96.0 |
|
0.05 |
89.9 |
|
0.10 |
84.7 |
|
0.25 |
72.9 |
|
0.50 |
62.2 |
|
0.75 |
57.9 |
|
1.00 |
56.9 |