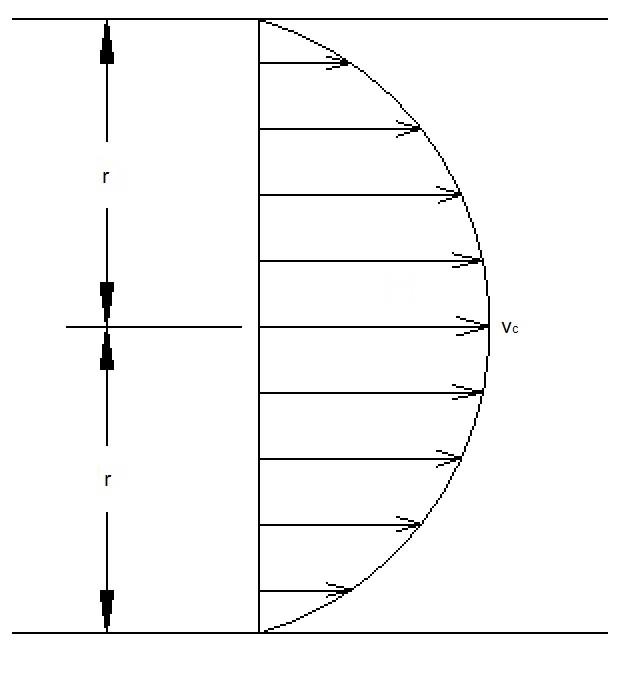
Fully developed flow occurs when the viscous effects due to the shear stress between the fluid particles and pipe wall create a fully developed velocity profile. In order for this to occur the fluid must travel through a length of a straight pipe. In addition, the velocity of the fluid for a fully developed flow will be at its fastest at the center line of the pipe (equation 1 laminar flow). On the other hand, the velocity of the fluid at the walls of the pipe will theoretically be zero. As a result, fluid velocity should be expressed as an average velocity.
(Eq 1) $v_C = \frac{2Q}{πR^2}$
vc = Maximum Velocity
Q = Flow Rate
R = Pipe Radius
As mentioned earlier the viscous effects are caused by the shear stress between the fluid and the pipe wall. In addition, shear stress will always be present regardless of how smooth the pipe wall is. Also, the shear stress between the fluid particles is a product of the wall shear stress and the distance the particle is from the wall. To calculate shear stress use equation 2.
(Eq 2) $τ=\frac{2τ_wr}{D}$
τ = Shear Stress
τw = Shear Stress at the Wall
r = radial distance from the center of the pipe to point of interest
D = Pipe Diameter
Due to the shear stress on the fluid particles, a pressure drop will occur. To calculate the pressure drop use equation 3.
(Eq 3) $P_2=P_1-ΔP$
Finally, the viscous effects, pressure drop, and pipe length will affect the flow rate. To calculate the average flow rate, you will need to use equation 4. This equation only applies to laminar flow.
(Eq 4) $Q=\frac{πD^4ΔP}{128μL}$
L = Pipe Length
μ = Dynamic Viscosity
Entrance Length and Fully Developed Flow
At first the fluid is not fully developed when it enters a pipe. Instead the fluid has to travel a certain distance undisturbed before it becomes fully developed. This is also true when a fluid goes around a curve in the pipe system. This is because the curve will disrupt the velocity profile of the fluid. As a result, it will need to travel a certain distance in a straight pipe to become fully developed again. Refer to equation 5 to calculate the entrance length for laminar flow, and equation 6 to calculate the entrance length for turbulent flow.
(Eq 5) $\frac{L}{D}=0.06·Re$
L = Entrance Length
D = Pipe Diameter
Re = Reynolds Number
(Eq 6) $\frac{L}{D}=4.4(Re)^{1/6}$
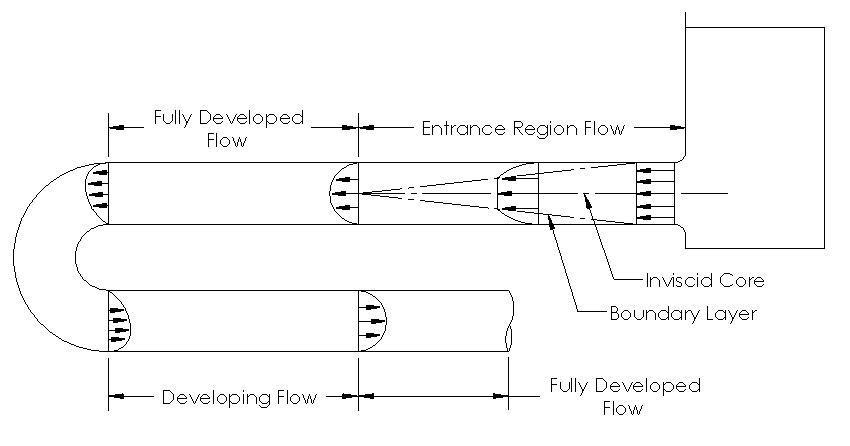
Notice from the diagram that a boundary layer starts to form as the flow becomes developed. The boundary layer represents where the viscous effects are produced along the pipe wall to create the velocity profile. Also notice while the flow is developing there is a region where there is no viscous effects; this is called the inviscid core.