For a fluid to flow through a pipe some type of force must drive it. Gravity is one force that will drive a flow. On the other hand a pressure difference, $Δp=p_1-p_2$, will also drive a flow. However, at some point the fluid flow will reach a steady average velocity. This is due to the viscous effects caused by shear stress. As a result, when the pressure forces equal the shear stress they will balance each other out causing a steady average velocity. Hence, if viscous effects did not exist, the fluid would continuously accelerate due to gravity or a pressure difference.
Non-Developed Fluid Flow Regions
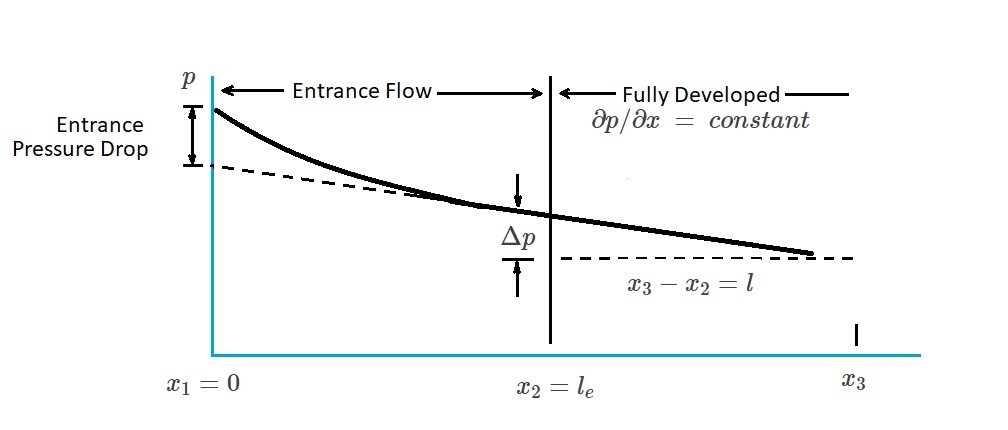
An example of a non-developed fluid flow region would be the entrance region. In this region the fluid will accelerate or decelerate as the velocity profile becomes developed. As a result there will be a balance between pressure, viscous, as well as inertial forces in the entrance region. In order for this balance to occur, there will need to be pressure distribution along the pipe. This will result in a pressure gradient that is larger in the entrance regions than the fully developed region, $∂p/∂x=-Δp/l<0$ In turn, this non-zero pressure gradient creates the viscous effects. The figure below shows the pressure drop from entrance region to the fully developed flow region for a horizontal pipe.
(Eq1) $x_3-x_2=l$
Laminar and Turbulent Flow
How the fluid flows though a pipe has a strong tie to whether the flow is laminar or turbulent. The reason for this is because of shear stress. For laminar flow, the resulting shear stress is a direct result of the momentum of the randomly moving molecules. On the other hand, for turbulent flow, the shear stress is caused by the momentum of the random movement of finite-size fluid particles. As a result, the shear stress for turbulent flow will be quite different in comparison to laminar flow. Finally, in addition to shear stress, the velocity profile will also be different between laminar and turbulent flow.