As a particle moves along a streamline and its velocity changes an acceleration along a streamline will occur. To understand acceleration along streamline it is helpful to use a coordinate system to define the streamline. Two examples of coordinate systems are the Cartesian and the polar coordinate system. First, the Cartesian coordinate system considers x, y, and z directions. On the other hand, the polar coordinate system considers the radius r, and angle θ from a specific origin.
In order to define a streamline, a streamline coordinate system is used to show the motion of a fluid particle. It does this by using unit vectors in two directions. One direction is along the streamline $\hat{s}$, while the other is normal to the streamline $\hat{n}$. Since a streamline coordinate system is expressed this way, the direction of these two vectors will change in respect to the Cartesian Coordinate system. This is because of the fact that the two vectors must either be tangent to the streamline or normal to the streamline, while the direction of the streamline can change itself.
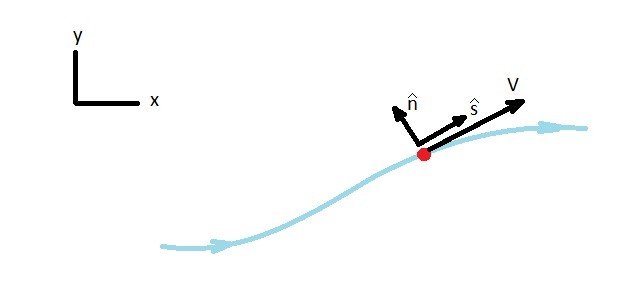
Acceleration along a Streamline
To determine the acceleration along a streamline you need to think about Dynamics. What happens when a particle accelerates around a curve? If a particle is accelerating around a curve there will be a normal ($\hat{n}$) and possibly a tangential ($\hat{s}$) acceleration. As a result, as a fluid particle moves along a streamline a tangential and normal acceleration could develop. This would result in the following equation.
(Eq 1) $ a = \frac{Dv}{Dt} = a_s\hat{s}+a_n\hat{n}$
It is important to realize that there is a difference, besides their direction, between normal and tangential acceleration. This difference is how the two acceleration occur. First, let’s talk about tangential acceleration. A tangential acceleration occurs the way any other acceleration would occur. There has to be a change in velocity of the fluid particle along the streamline in relation to time. As a result a tangential acceleration will be produced. To determine a tangential acceleration the following equation would be used.
(Eq 2) $a_s=v\frac{∂v}{∂s}$
Now we have to look at normal acceleration. Normal acceleration behaves differently than other types of acceleration. It will occur regardless of if the velocity is changing with time or if the velocity is constant. Instead it occurs because the particle is changing direction. As a result a normal acceleration will occur when there is a curve in a streamline. Its value will be based off of the current particle velocity and radius (r) of the streamlines curve.
(Eq 3) $a_n = \frac{v^2}{r}$
Finally, the total acceleration of the fluid particle can be found by finding the magnitude of the tangential and normal acceleration.
(Eq 4) $a=\sqrt{a_s^2+a_n^2}$