Observing a fluid in motion will allow you to make the general statement that it flows from one point to another. In turn this will result in a net motion of particles. A function of time can be used to describe the particle motion from one point in space to another. As a result a function of time will allow us to describe the velocity of each particle along its path. Further more as we continue to describe particle velocities we will generate a velocity field that will describe the motion of all of the particle.
Continuum Hypothesis
Now in reality it would be impossible to describe each individual particle velocity along its path. To overcome this challenge we can use the continuum hypothesis. The continuum hypothesis takes in consideration that particles will interact with each other as well as their surroundings. As a result each particle can contain numerous fluid molecules. This will allow us to describe flow as the motion of fluid particles instead of individual fluid molecules. The continuum hypothesis also applies to the fluid particle acceleration not just fluid particle velocity.
Finally, when you are considering the other fluid properties such as density, you can consider them as a function of the fluid particle’s location. This is because the fluid particle’s created by the continuum hypothesis are packed tightly together. They are also infinitesimally small. Representing additional fluid properties through spacial coordinates is known as field representation of the flow. It is important that you also realize that the field representation can change due to time. As a result not only are they a function of spatial coordinates but also of time. For example if we were to specify temperature, the temperature field would be the following. $T=T(x,y,z,t)$
Velocity Field
Just like the temperature field you can describe the velocity field the same way. $v = v(x,y,z,t)$ Further more you can also break this statement into vector form.
$v = u(x,y,z,t)\hat{i}+ν(x,y,z,t)\hat{j}+w(x,y,z,t)\hat{k}$
Where $u$, $ν$, and $w$ are the x,y, and z velocity vector components. The position of a fluid particle vector can described using the coordinate system. Refer to the image below.
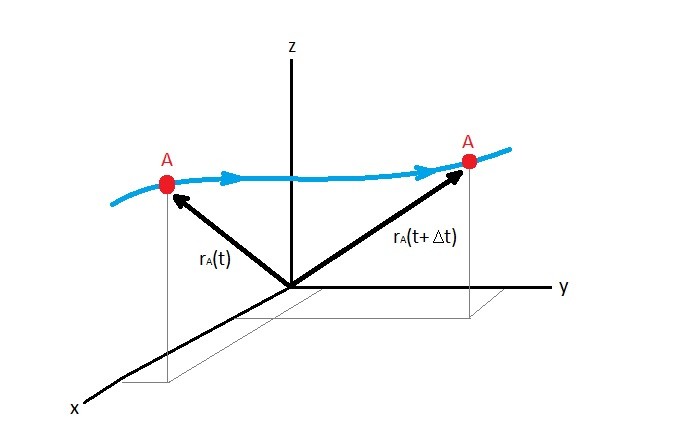
The velocity can be determine by taking the time derivative of the position, $\frac{dr_A}{dt}$. Now since we live in a three dimensional world. As a result you may need to know what the velocity is in each direction. To find the total velocity you will need to find the magnitude of the these velocities. To do that you would use the following equation.
$v=\sqrt{u^2+ν^2+w^2}$
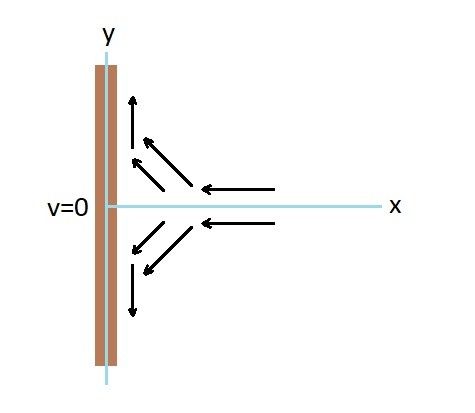
Finally, when analyzing the velocity field of a fluid you must remember that external geometry will effect how the overall bulk fluid flows. As a result when the fluid encounters an object there will be different paths that the fluid particle could take. Unless the flow is turbulent, the fluid particle will follow the same path as the particle in front of it but not necessarily the same path as the particle next to it which could be on a different path. On the other hand if the flow is turbulent than what was stated above becomes more complicated since eddies will develop. Below is a 2-dimensional example of the paths fluid particles could take if it were to encounter and obstruction like a wall.