Up until this point I have only discussed motion that is following a straight path. However, a particle can also follow a curved path. As a particle moves around a curved path it can experience a normal and tangential force.
Tangential Force
First, a tangential force is a result of a tangential acceleration which is always perpendicular to radius coming from the axis of rotation. In order for there to be a tangential force there has to be a change in tangential velocity.
(Eq 1) $∑F_t = ma_t$
m = mass
at = tangential acceleration
ft = tangential force
Normal Force
Next, a particle going around a curve will always have a normal force. The reason for this is because there is a change in direction, and in order to change a particles direction a force needs to act on it. The normal force is always pointing towards that axis of rotation.
(Eq 2) $∑F_n = ma_n$
an = normal acceleration
fn = normal force
Remember, to find the normal acceleration of a particle you will need to know the particles angular velocity as well as the distance it is from the axis of rotation.
(Eq 3) $a_n=\frac{v_t^2}{r}$
Finally, to find the resultant force of both the normal and tangential force, you would need to take the magnitude of the two forces.
(Eq 4) $F_R=sqrt{F_t^2+F_n^2}$
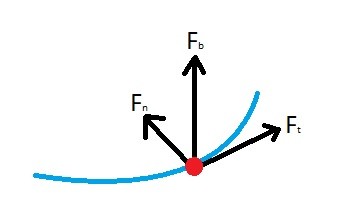
Binormal Force
Finally, to be thorough, we must also analyze the binormal vector. The binormal vector is the vector that is perpendicular both the normal and tangential force vectors. You can see this in the image above. However, when analyzing these type of problems, there will never be a force in this direction. This means that the binormal force vector will always be zero, and the only forces that will be acting on the particle are the normal and tangential force.
(Eq 5) $∑F_b = 0$
$F_b$ = binormal Force
Example
As roller coaster goes around a corner normal acceleration will result. Determine the bank of the corner to so that the trains normal force will be directed directly into the track so that the safety wheels aren’t be used to keep the train on the track.

Solution
Step 1: Draw a free body diagram.
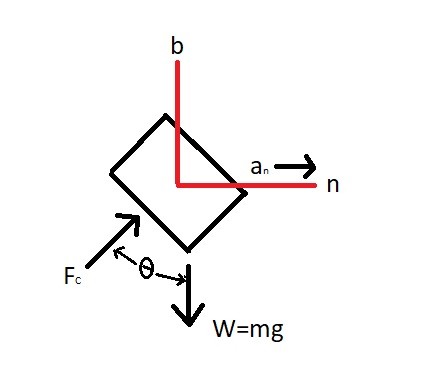
Step 2: Using the n, b axes define the equations of motion.
(1) $∑F_n=ma_n$: $F_csinθ=m\frac{v^2}{r}$
(2) $∑F_b=0$: $F_ccosθ-mg=0$ or $F_ccosθ=mg$
Step 3: Divide (1) by (2) and solve for θ
$\frac{F_csinθ=m\frac{v^2}{r}}{F_ccosθ=mg}=tanθ=\frac{v^2}{gr}$
$θ=tan^{-1}\left(\frac{v^2}{gv}\right)$