Newton’s second law is what allows us to determine the force caused by an acceleration. It states “the relation between an object’s mass m, its acceleration a, and the applied force F is F=ma, where acceleration and force are vectors, and the direction of the force vector is the in the same direction as the acceleration vector.” To simplify this statement, what it is say is if you have a problem that has multiple forces, you can find the resultant force of those force to determine the acceleration.
(Eq 1) $∑F=ma=F_R$
where
(Eq 2) $F_R=\sqrt{F_x^2+F_y^2+F_z^2}$
The image below shows how the resultant force caused by $F_1$ and $F_2$ is equal to mass times acceleration.
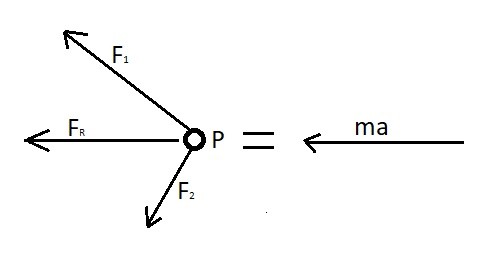
When solving a dynamics problem you should always draw a free body diagram. By doing this you be able to account for all the forces and determine the resultant force. After drawing a free body diagram and you find that all of the forces sum to zero than there will be no acceleration on the particle. As a result the particle will either remain stationary or its current velocity will not change.
You will also need to determine a Newtonian or inertial frame of reference effectively determine the affects of an acceleration. What this means is you need find a static reference point that cannot rotate and that is fixed or is moving at a constant velocity. As a result, by establishing an inertial frame of reference two different observers at two different location will be able to calculate the same resultant force.
Example
Determine the acceleration of the box in the image below. The box weights 250 Newtons, and the coefficient of kinetic friction is 0.2. There is a force of 300 Newtons pulling on the box at a 25 degree angle. It can be assumed that the surface the boxing is being pulled across is perfectly flat.
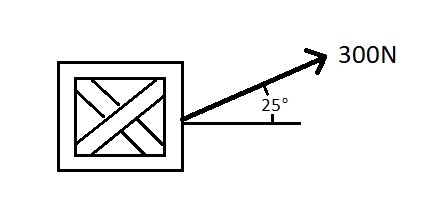
Solution
Step 1: Draw a free body diagram.
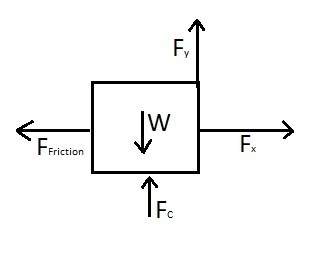
Step 2: Based off the free body diagram define the equations of motion.
$F_y+F_c-W=0$
$F_x-F_{fiction}+ma=0$
where $F_{friction}=0.2F_c$ and $m=\frac{W}{g}$
Step 3: Find the acceleration a
$F_c=W-F_y$$=250-300sin(25)=123.2 N$
$a=\frac{F_{friction}-F_x}{m}$$=\frac{24.64-300cos(25)}{-25.48}=9.7\frac{m}{s^2}$