Angular momentum is the moment of a particles linear momentum as the particle rotates around a point in space. Another term for angular moment is the moment of a momentum.
Scalar Formulation
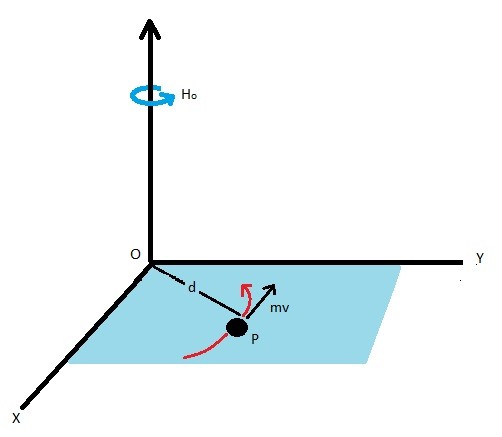
First let’s take a look at angular momentum that resides on a single plane. Let’s say the x-y plane. When this is the case, you can use a scalar equation to solve this problem. Equation 1 represents the scalar equation that you would use.
(Eq 1) $(H_O)_z=(d)(mv)$
d = the distance from the particles center of mass to the point of rotation
m = the particles mass
v = the particles velocity
Vector Formulation
Besides moving through one plane, a particle can also move through multiple planes. When a particle is moving through multiple planes, the problem will become more complicated. This is due to the fact that now you will have to look at three dimensions. When this is the case you will need to use vector algebra to solve the problem. Equation 2 represents the equation that you would use.
(Eq 2) $H_O = d×mv$$=\left|\matrix{i &j & k \cr d_x & d_y & d_z \cr mv_x & mv_y & mv_z}\right|$
Moment of a Force and Angular Momentum
Besides angular momentum, you can also determine the moments on a particle as it rotates around a point. By determining the moments acting on a particle you will be able to determine the forces that create the moment. You can determine a moment by multiply a force times a distance. In this case the distance is the distance from the point of rotation. Equation 3 represent the equation that would used to calculate a moment.
(Eq 3) $(M_O)_z=(F)(d)$
In order for you to use equation 3 the particle will have to be traveling on a single plane. In contrast, if you have case where the particle is traveling on multiple planes, you would instead use equation 4.
(Eq 4) $∑M_O = d×F$$=\left|\matrix{i &j & k \cr d_x & d_y & d_z \cr F_x & F_y & F_z}\right|$
To determine a force you will need to multiply the particles mass by its acceleration. In order for you to determine the particle acceleration you will need to take the derivative of the particle velocity in respect to time. To do this you would use equation 5.
(Eq 5) $a = \frac{d}{dt}v$
In order to relate angular momentum to a moment you will need to take the derivative of equation 2 in respect to time.
(Eq 6) $\frac{d}{dt}H_O = \frac{d}{dt}(r×mv)= \frac{d}{dt}r × mv + r×m\frac{d}{dt}v$
where $ \frac{d}{dt}r × mv = m(\frac{d}{dt}r×\frac{d}{dt}r) = 0 $
(Eq 7) $\frac{d}{dt}H_O = r×m\frac{d}{dt}v = ∑M_O$
Due to the fact that angular momentum is the moment of linear momentum, where L=mv, you could simplify equation 7 to the following.
(Eq 8) $∑F = \frac{d}{dt}L=m\frac{d}{dt}$
Notice that equation 7 and 8 are just another way of stating Newton’s second law of motion, F=ma.
Example
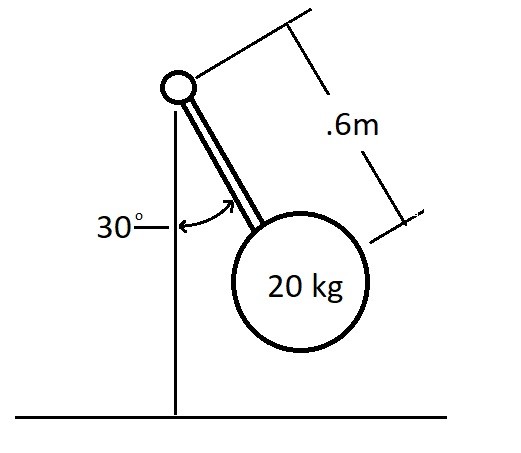
A 20 kg plat is attached to a rigid rod. The rods mass can be considered negligible in comparison the 20 kg plate. At its current position depicted in the image the plate is moving at 7 m/s. Determine the plates angular momentum at its current position. Determine the rate that its velocity is increasing at its current point.
Solution
Step 1: Draw a free body diagram.
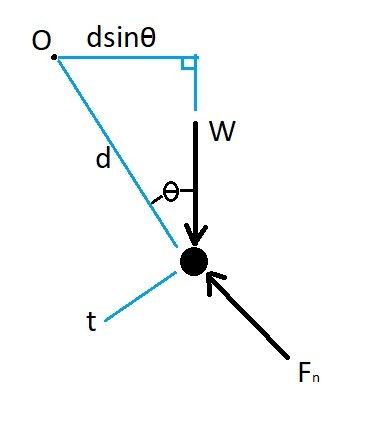
Step 2: Determine the angular momentum of the plate.
$H_O=dmv$$=(0.6)(20)(7)= 84 \frac{kg·m^2}{s}↓$
Step 3: Determine the rate the velocity will increase.
$↑+∑M_O=\frac{d}{dt}H_O$
$mgdsinθ=dm\frac{dv}{dt}$
$\frac{dv}{dt}=gsinθ$$=9.81sin(30)=4.905\frac{m}{s^2}$