There are two distinct forms of energy that will transfer between a system and its surroundings. These forms of energy are heat and work. In the previous article I discussed heat energy. However, for this article I will be focusing on work energy.
What is Work Energy
Work is an energy transfer between the system and it surroundings that is not caused by a temperature difference. Hence, to be more specific, work energy is associated with a force that is acting through a distance. Some examples of this would be a moving piston, a rotating shaft, or a live electrical wire that crosses the boundary layer of the system.
The units of work like all forms of energy, is expressed as kJ for the standard international system. In addition, work can be expressed as a per unit mass.
(Eq 1) $w=\frac{W}{m}$ (kJ/kg)
Finally, when work is expressed per unit time this is called power. The standard international unit for power is kJ/s, or kW.
Like heat, work is a directional quantity. Hence, in addition to being expressed as a magnitude, it also needs to be expressed in such a way to denote its direction. This can be done by using sign convection. For example you could use a positive sign to represent the work that is done by a system. As a result, work that is done on system must be represented by a negative sign. In addition, instead of using positive and negative signs you could also use the subscripts in and out.
Finally, since heat and work are both energy transfer mechanisms, there are many similarities between the two. First, both recognize the boundary layer of a system. Next, a system possesses energy not heat or work. Third, both heat and work are associated with a process not a state. This means that neither heat or work have a meaning at a state. Finally, both heat and work are path functions. In other words, their magnitude is dependent on the path they follow during a process.
Electrical Work
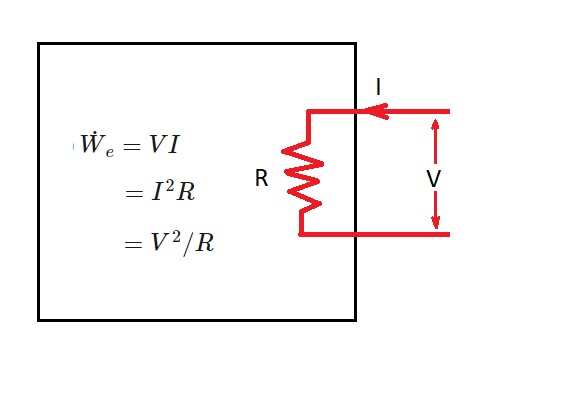
Mechanical work is not the only type of work energy that can cross the boundary layer of a system. There can also be electrical work on a system. The reason for this is because in order for electrons to move through a wire there must be electromotive forces. In turn, these electromotive forces cause electrical work energy. This is because there is $N$ coulombs of electrical charge that is moves from a potential difference $V$.
(Eq 2) $W_e=VN$ (kJ)
In addition, equation 2 can be expressed as per unit time to define electrical power.
(Eq 3) $\dot{W}_e=VI$ (W)
$I$ = electrical current
Finally, you can take take the integral of equation 3 in respect to time to also define electrical work.
(Eq 4) $W_e = \int{}^2_1VIdt$ (kJ)
This equation can be simplified if both voltage $V$ and current $I$ are constant.
(Eq 5) $W_e = VIΔt (kJ)