Understanding different forms of energy is very important. Some examples are mechanical, kinetic, potential, chemical, thermal, and nuclear energy. It is possible that a system could have a multitude of different forms of energy within it. As a result, the sum of these different forms of energy will result in the total energy of the system.
(Eq 1) $e=\frac{E}{m}$ (kJ/kg)
When you are determining the different forms of energy within a system you will need to look at the system at a macroscopic level as well as a microscopic level. A macroscopic level represents system processes as a whole in respect to an outside reference frame. Potential as well as kinetic energy occur at the macroscopic level. On the other hand, microscopic forms of energy represent the energy that effects the molecular structure of the system. In turn, microscopic forms of energy are independent of the system’s outside reference frame. Finally, the internal energy, $U$, of a system represents the sum of the microscopic forms of energy within the system.
Kinetic Energy
As a system is in motion it possesses a macroscopic form of energy called kinetic energy. A system’s kinetic energy is the result of the system’s velocity, $v$, and its mass, $m$. If all of the parts within the system are moving at the same velocity, than the kinetic energy is determined by using the following equation.
(Eq 2) $KE=m\frac{v^2}{2}$ (kJ)
In addition, kinetic energy can be expressed as a per unit mass.
(Eq 3) $ke=\frac{v^2}{2}$ (kJ/kg)
Finally, to find the kinetic energy of a rotating body the following equation is used.
(Eq 4) $KE=\frac{1}{2}Iϖ^2$ (kJ)
$I$= mass moment of inertia
$ϖ$ = angular velocity
Potential Energy
Another form of Energy is called Potential Energy. This represents a stored energy. This stored energy could be a result of an object being held at a certain height in a gravitational field, $g$. In addition, holding a spring in a compressed or stretched state is a form of potential energy. For right now let’s focus on potential energy do to elevation, $z$.
(Eq 5) $PE=mgz$ (kJ)
The equation above represents the potential energy caused by an elevation.
In addition, as with kinetic energy, potential energy can be expressed as a unit mass basis.
(Eq 6) $pe=gz$ (kJ/kg)
Internal Energy
Internal energy is the total sum of all microscopic forms of energy within a system. More precisely we are looking at the molecular structure as well as the molecular activity of the system. In other words, we are now considering the kinetic and potential energy of individual atoms and molecules.
Different forms of internal energy are sensible energy, latent energy, chemical energy, and nuclear energy.
Sensible Energy
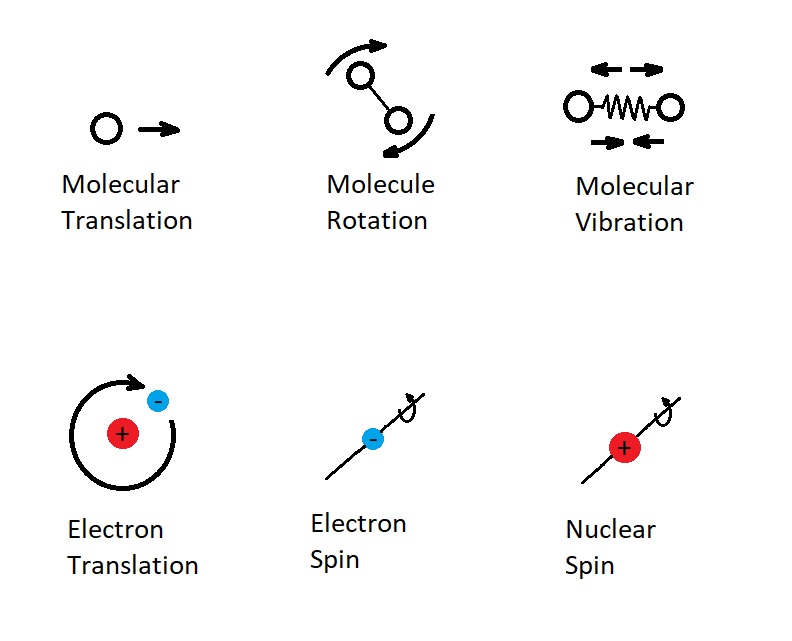
First, let’s take a look at sensible energy. Sensible energy is the portion of internal energy that is associated the various kinetic energies of the molecules and atoms. For example, there can be translational kinetic energy. This occurs when a molecule is moving in a straight line. In addition, there is also rotational kinetic energy. Rotational kinetic occurs as the molecules rotate. Finally, there can also be vibrational kinetic energy, which is caused by the molecules vibrating.
In addition, to molecules, atoms also can have sensible energy. One example of this is the electrons spinning around the atoms nucleus. In addition, electrons can also spin around their own axis creating kinetic energy. Finally, the particles within the nucleus can also spin.
For both molecules and atoms, the amount of sensible energy is directly proportional to temperature. This means the higher the temperature the higher the sensible energy. The image below shows the different types of sensible energy.
Latent Energy
Next, latent energy represents the binding force between molecules, atoms within a molecule, and the particles within an atom. This binding force is at its strongest when the substance is a solid and becomes weaker as it transitions from solid to liquid to gas. As a result, latent energy is directly responsible for the phase change processes of a substance.
Chemical Energy
Next, chemical energy represent the atomic bonds between the electrons of the atoms within a molecule. When a chemical reaction occurs these chemical bonds are destroyed causing the molecule to break apart. However, while this occurs different chemical bonds can form creating a completely new molecule. When this occurs the internal energy of the system will change.
Nuclear Energy
Finally, nuclear energy represents the energy that holds the nucleus of an atom together. These bonds represent a tremendous amount of energy. However, for most thermodynamics problems you will not need to worry about the nuclear energy. The only time nuclear energy needs to be considered is if a fusion or fission reaction is occurring. Fusion occurs when two smaller atoms are pushed together to create a new larger atom. On the other hand, fission occurs when a large atom is split apart creating smaller atoms.
Total Energy
The total energy is calculated by taking sum of the potential energy, kinetic energy, and internal energy of the system.
(Eq 7) $E = U+KE+PE$ (kJ)
In addition, the total energy can also be written as a unit mass basis.
(Eq 8) $e=u+ke+pe$ (kJ/kg)
For a closed system, the system will normally remain stationary. As a result, there will be no change in the kinetic or potential energy of the system. Hence, the change in total energy will be same as the change in internal energy.
On the other hand, control volumes normally involve a fluid flow. As a result, energy is normally associated with the mass flow rate $\dot{m}$. The mass flow rate is related to the volume flow rate, $\dot{V}$, of a fluid and the density, $ρ$, of the fluid.
(Eq 9) $\dot{m}=ρ\dot{V}=ρA_cv_{avg}$ (kg/s)
$A_c$ = cross-sectional area
Finally, the energy flowrate can be determine by multiplying the total energy per unit mass by the mass flow rate.
(Eq 10) $\dot{E} = \dot{m}e$
Mechanical Energy
Both kinetic and potential energy are forms of mechanical energy. However, thermal, nuclear, and chemical energy are not. In addition, most mechanical systems do not produce a significant amount of heat. Instead these systems generally operate at a constant temperature.
Mechanical energy is a form of energy that is converted to mechanical work by a mechanical device. An example of a mechanical device could be a pump or turbine. A pump is uses mechanical energy to increase the pressure of a fluid. In turn, this will move the fluid. On the other hand, a turbine is used to extract energy from a fluid by lowering the pressure of the fluid. As a result, the pressure within a flowing fluid is is associated with mechanical energy.
It is important to note that even though pressure is associated with mechanical energy, pressure itself is not a form of energy. Instead a pressure force acting on a fluid through distance is a form of work energy. This often referred to as flow work. It is also part of the energy associated with a flowing fluid, which is called flow energy. To find the total flow energy of a fluid the following equation is used.
(Eq 11) $e_{mech}=\frac{p}{ρ}+\frac{v^2}{2}+gz$
This equation is the Bernoulli equation of fluid mechanics. Bernoulli equation is sometimes referred to as the energy equation in fluid mechanics. In this equation $p/ρ$ is the flow energy, $v^2/2$ is the kinetic energy, and $gz$ is the potential energy of the fluid. This equation can also be expressed in a mass flow rate form.
(Eq 12) $\dot{E}_{mech}=\dot{m}e_{mech}=\dot{m}\left(\frac{p}{ρ}+\frac{v^2}{2}+gz\right)$