The two main forms of energy are work and heat. Work is a form of energy that doesn’t require a temperature differences between the system and its surroundings to transfer across the boundary layer. In addition, there are several different ways of doing work. One form of work is mechanical work.
Mechanical Work
First, what is work? Works is done by applying a force $F$ on a body to displace it a certain distance $s$.
(Eq 1) $W=Fs$ (kJ)
In addition, if the force is not constant:
(Eq 2) $W=\int{}^2_1~F~ds$ (kJ)
Next, we need to look at what happens when there is work interaction between a system and its surroundings. For this to occur, first the force must be acting on the boundary. After that the boundary must move a certain distance. If the boundary does not move than there hasn’t been a work interaction between the system and its surroundings. So how does this interaction occur. Well one way is through mechanical work. There are many different forms of mechanical work. However, for right now I am going to focus on shaft work, spring work, acceleration of a moving body, and a force being applied to a solid elastic body.
Shaft Work
There are a fair amount of real world examples when mechanical energy is transferred through a rotating shaft. One example that you see every day is your car. As a car runs the energy from the engine move through transmission to the drive shaft which is connected to the wheels. Through that system there is a series of rotating shafts transferring the engines energy to the wheels of the car.
In order to transfer mechanical energy through a shaft, a torque $T$ must be applied to it. A torque is a force $F$ acting on a moment arm $r$.
(Eq 3) $T=Fr$
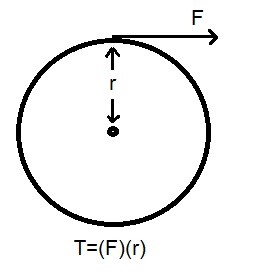
As the force is applied to the moment arm it will act through a distance $s$. This distance is related to the radius $r$ of the shaft through the following equation.
(Eq 4) $s=(2πr)n$
$n$ = number of revolutions
Finally, since we know the distance the rotating shaft has traveled, we can now determine the mechanical work of the shaft.
(Eq 4) $W_{sh}=Fs=\left(\frac{T}{r}\right)(2πrn)=2πnT$ (kJ)
Next, we can determine the power transmitted through the shaft by determining the number of revolutions per unit time $\dot{n}$.
(Eq 5) $\dot{W}_{sh}=2π\dot{n}T$ (kW)
Spring Work
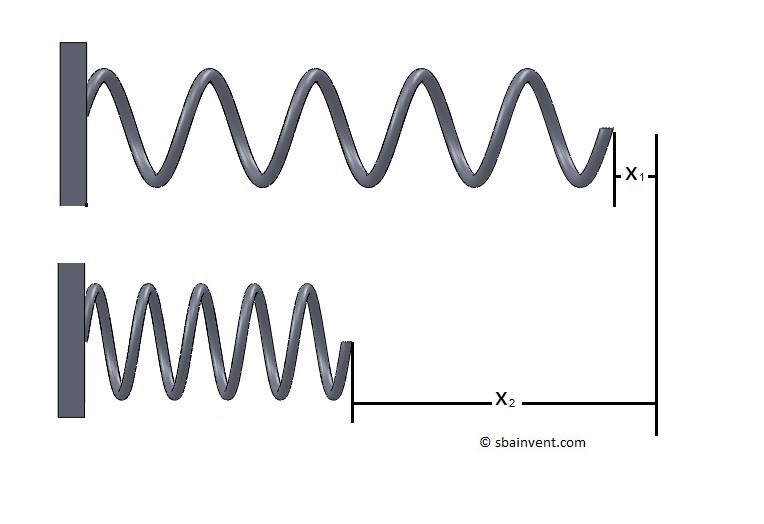
As a force is applied to a spring the length of the spring will change. In order for this to occur work must be done.
(Eq 6) $δW_{spring}=Fdx$ (kJ)
In addition, to relate the force $F$ to the displacement $x$ we will need to determine the spring constant $k$. As a result, if the force and displacement are linearly related, than the following equation is used to determine the spring constant.
(Eq 7) $k=\frac{F}{x}$
Finally, taking a linear spring constant into consideration equation 6 will become the following.
(Eq 8) $W_{spring}=\frac{1}{2}k(x^2_2-x^2_1)$ (kJ)
$x_1$= initial displacement
$x_2$ = final displacement
Solid Elastic Body
A solid elastic body is essentially a stiff linear spring. As a force is applied to it, it will either contract or elongate. In addition, when that force is released, as long as the stress on the body stayed within the elastic range, it will return to its original shape. However, if the stress on the body is greater than the yield strength, the body will permanently deform, keeping it from returning to its original shape.
Due to the fact that an elastic body behaves like a linear spring, the same equations used to determine the work on a spring are used.
As a result,
(Eq 9) $W_{elastic} = \int{}_1^2~F~dx=\int{}^2_1~σ_nA~dx$ (kJ)
$σ_n$ = normal stress
$A$ = cross-sectional area
Work to Accelerate a Body
As a body is accelerates the kinetic energy of that body will increase. However, in order for this to occur energy must be transferred into the body. This can be done through either heat or work. Yet in this case the energy transfer cannot occur due to heat since it is not driven by a temperature difference. As a result, the energy is transferred through work.
In order to determine the work to accelerate an object on a flat surface the following equation would need to be used.
(Eq 10) $W_a=\frac{1}{2}m(v^2_2-v^2_1$ (kJ)
$v_2$ = final velocity
$v_1$ = initial velocity
$m$ = mass
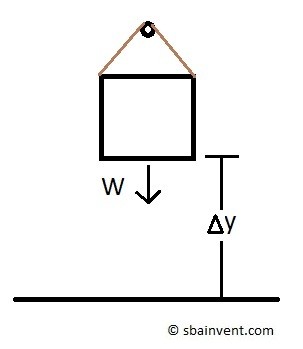
Work to Raise a Body
Finally, as a body is raised a certain distance potential energy will be stored. That energy has to come from heat or work. However, since this isn’t be driven by a temperature difference, the energy has to be transferred through work.
As a result,
(Eq 11) $Wg=mg(h_2-h_1)$
$g$ = gravitational constant
$h_2$ = final height
$h_1$ = initial height