Heat Transfer: Natural Convection

Convection can occur in two different ways. One method is forced convection. Forced convection is occurs when a fluid is forced over a surface or through piping, such as a fan blowing air over a plate or fluid being pumped through the pipes of a heat exchanger. It can also occur naturally. Natural convection occurs when fluid moves over a surface due to density changes in the fluid. An example of natural convection is base board heating. As the heater heats up the air around it the hot air will rise. This air will than be replaced by cooler air. This causes air flow over the surface resulting in natural convection.

Like any type of fluid motion there will be a boundary layer that is formed in the fluid as it moves over the surface. The image below shows the boundary layer of fluid as it moves over a flat plate due to natural convection.

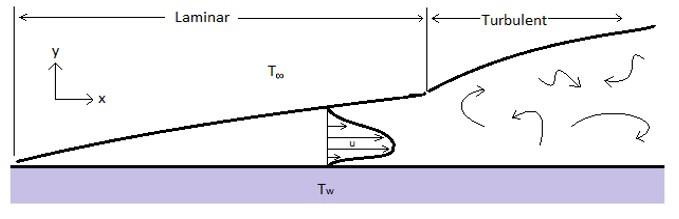
Just like forced convection over a flat plate, the flow will initially be laminar but as it continues over the length of the plate turbulent eddies will begin to form until the flow becomes fully turbulent. Unlike forced convection, the air flow for natural convection is much lower than forced convection, which will result in a lower convection heat transfer coefficient. The boundary layer as seen in the image also differs. The fluid velocity will go to zero at the surface of the plate, which is simular to forced convection, however, it also goes to zero at a certain point in the fluid surounding the plate, which is different than forced convection. The maximum fluid velocity occurs in the first 1/3 of the bound layer coming of the surface of the plate.

To determine whether the fluid is laminar or turbulent for forced convection Reynolds number was used. However, for natural convection Grashof number will be used. The Grashof number represents the ratio of buoyancy forces to viscous forces for free convection. For natural convection across a vertical flat plate the critical Grashof number before the fluid starts to transition to turbulent flow is 4 X 10⁸. To calculate the Grashof number the following equation would be used.

(Eq 1) $Gr_x=\frac{gβ(T_w-T_∞)}{ν^2}$

 

g = gravitation constant (9.81 m/s²)

x = distance along plate

T_w = Wall temperature

T_∞ = Fluid Temperature

ν = kinematic viscosity

β = Volume Coefficient of Expansion

To calculate the volume coefficient of expansion the following equations can be used.

(Eq 2) $β=\frac{ρ_∞-ρ}{ρ(T-T_∞)}$

ρ =Fluid Density on Surface

ρ_∞ = Ambient Fluid Density

(Eq 3) $β=\frac{1}{T}$

Equation 3 can only be used for ideal gases, where T represents the absolute temperature of the gas.

To determine the convective heat transfer coefficient for natural convection the following equation will be used.

(Eq 4) $h=\frac{Nu_xk}{x}$

Nu_x = Nusselt number

k = thermal conductivity of the fluid

For equation 4 there are a variety of equations that can be used to determine the Nusselt number. To determine which equation to use you will need to know the restriction that apply to each equation. The first thing that you will need to determine is what the Rayleigh number is. The Rayleigh number represents the product of the Grashof number and the Prandtl number. Refer to the equations below.

(Eq 5)  $Ra=GrPr$

Pr = Prandtl number

(Eq 6) $Pr=\frac{c_pμ}{k}$

Prandtl number can be calculated using equation 6, it can also be found in the appendix of most heat transfer books.

The next restriction that needs to be considered is whether temperature on the surface of the object is isothermal or due to a constant heat flux. Finally, the shape of the surface that the fluid is flow over needs to be considered.

Below are Nusselt number equations that would be used for an isothermal equation.

(Eq 7) $\overline{Nu} = \sqrt{0.825+\frac{0.387Ra^{1/6}}{[1 + (0.492 / Pr)^{9/16}]^{8/27}}}$

Restrictions: 10^-1 < Ra_L < 10¹² , Vertical Isothermal surface

(Eq 8) $\overline{Nu}=\sqrt{0.60+0.387\left(\frac{GrPr}{[1+(0.559 / Pr)^{9/16}]^{16/9}}\right)^{1/6}}$

Restrictions: 10^-5 < GrPr < 10¹³, Isothermal horizontal cylinders

(Eq 9) $Nu_f=C(Gr_fPr_f)^m$

Restrictions: Isothermal surface, refer to the tables below to determine the values for C and m.

Vertical Planes and Cylinders

The next surface condition to consider would if there was a constant heat flux on the surface. To find the Nusselt number for a vertical surface with a constant heat flux the following equation would be used.

(Eq 10)  $Nu_{xf}=C(Gr^*_xPr_f)^m$

Restrictions:

C=0.60, m= 1/5 for 10^-5 < Gr*_x Pr < 10¹¹

C = 0.17, m = 1/4 for 2 X 10¹³ Gr*_x Pr <10¹⁶

(Eq 11)  $Gr^*_x=\frac{gβq_wx^4}{kν^2}$

Equation 10 is used for a specified distance on a surface and does not consider the entire length of the surface. To determine the average heat transfer for the whole surface for a constant heat flux on a vertical surface the following equation would be used.

(Eq 12)  $\overline{h}=\frac{5}{4}h_{x=L} $

for $q_w=const$