There will be a time when you have to be able to calculate the total heat transfer for a problem that has both convection and conduction. Recall that the heat transfer equation for conduction is the following.
(Eq 1) $q = -kA\frac{ΔT}{Δx}$
k = Thermal Conductivity
A = Cross-Sectional Area Perpendicular to Heat Flow
T = Temperature
x = thickness of interest in the direction of the heat flow
The heat transfer equation for convection is the following.
(Eq 2) $q = hA(T_w-T_∞)$
h = Convection Heat Transfer Coefficient
A = Surface Area
Tw = Temperature on the Objects Surface
T∞ = Fluid Temperature
Below is an image showing a case where both conduction and convection are taking place.
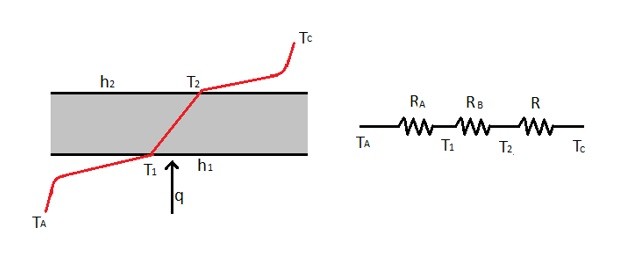
Taking the above image into consideration equation 1 and 2 can be modified to the following equation.
(Eq 3) $q = h_1A(T_A-T_1) = \frac{kA}{Δx(T_1 – T_2)} = h_2A(T_2 – T_C)$
From equation 3 it can be seen that the two convection properties and the conduction property all have the same heat flow going through them. This means that each of their individual thermal resistances are added up to a total system resistance. To calculate the individual thermal resistance for convection and conduction the following equations would be used.
(Eq 4) $R_{convection} = \frac{1}{hA}$
(Eq 5) $R_{conduction} = \frac{Δx}{kA}$
The above image has the thermal resistances in series. To determine the total thermal resistance the following equation would be used.
(Eq 6) $R_{TOT} = R_A + R_B + R_C = \frac{1}{h_1A} + \frac{Δx}{kA} + \frac{1}{h_2A}$
Once the total system resistance is determined the total heat transfer across the system can be determined using the following equation.
(Eq 7) $q = \frac{T_A-T_C} {R_{TOT}}$