Recall that convective heat transfer occurs when there is a fluid flowing over a body. To calculate the heat transfer rate the following equation would be used.
(Eq 1) $q = hA(T_w-T_∞)$
In the above equation h represents the convective heat transfer coefficient. To determine what this value is you will need to have an understanding of laminar and turbulent flow. Laminar flow occurs when there are distinct fluid layers through the boundary layer of the fluid. As the fluid velocity increases the flow will start transition into turbulent flow. Once the flow is fully turbulent the fluid layers will no longer be observed and instead will become random. For heat transfer purposes turbulent flow will transfer heat better than laminar flow will. Below shows fluid flow over a flat plate.
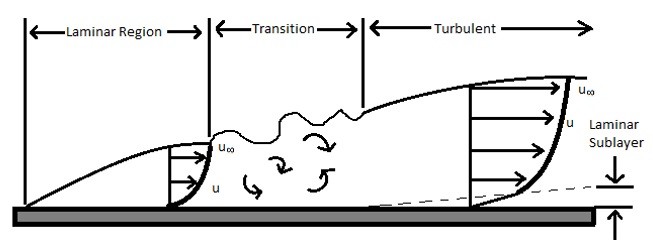
In order to determine if a flow is laminar or turbulent Reynolds number would be used. For a flat plate and if the flow is less than 5 X 105 than the flow is in the laminar range. If the Reynolds number is in between 5X105 and 106 the flow is transitioning from laminar to turbulent. Finally if the Reynolds number is higher than 106 the flow is Turbulent. To calculate the Reynolds number for a flat plate the following equation will be used.
(Eq 2) $Re_x =\frac{u_∞x}{ν}$
u∞=free stream velocity
x=distance from leading edge
ν=kinematic viscosity
If you want to know the Reynolds number for the entire length of plate, the length L of the plate will replace the variable x in the above equation.
Notice that in addition to fluid flow, the length of the plate dictates when the fluid will transition from laminar to turbulent flow. This means that initially when fluid starts flowing over the plate the fluid will be in a laminar state and then will transition to a turbulent flow.
In order to calculate the convective heat transfer coefficient Prandtl number will need to be used as well as Nusselt number. Prandtl number is used to relate the fluids viscosity to the specific heat of the fluid and the thermal conductivity of the fluid. The equation below can be used to calculate Prandtl number. Prandtl number can also be found in the Appendix of most Heat Transfer books.
(Eq 3) $Pr = \frac{C_pμ}{k}$
Nusselts number on the other hand is used to relate the thermal boundary layer to the fluid flow boundary layer. Depending on the boundary conditions, the equations for Nusselts number will differ. The equations below are used to calculate Nusselts number for a flat plate based off of various restrictions.
The Nusselts equations below are used when the flow is laminar.
(Eq 4) $Nu_x = 0.332Pr^{1/3}Re_x^{1/2}$
Restrictions: Tw=const, Rex <5×105, 0.6 < Pr < 50
(Eq 5) $Nu_x =\frac {0.3387Pr^{1/3}Re_x^{1/2}}{[1 + (0.0468/Pr)^{2/3}]^{1/4}}$
Restrictions: Tw=const, Rex < 5×10 5 , PrRex > 100
(Eq 6) $Nu_x = 0.453Pr^{1/3}Re_x^{1/2}$
Restrictions: qw=const, Rex <5×105, 0.6 < Pr < 50
(Eq 7) $Nu_x=\frac{0.4637Pr^{1/3}Re_x^{1/2}}{[1+(0.0207/Pr)^{2/3}]^{1/4}}$
Restrictions: qw=const, Rex < 5×10 5
(Eq 8) $Nu_x = 0.332Pr^{1/3}Re_x^{1/2}\left[1 – \left(\frac{x_o}{x}\right)^{3/4}\right]^{-1/3}$
Restrictions: Tw=const, starting at
x=xo, Rex <5×105 , 0.6 < Pr < 50
(Eq 9) $\overline{Nu}_L = 2Nu_{x=L}$
Equations 4 and 5 are used when the surface of the plate is isothermal, meaning that it is at the same temperature. Equations 6 and 7 are used when there is a constant heat flux on the surface of the plate. Equation 8 can be used when the plate has an unheated starting edge, xo will be the point on the plate where the heating starts, while x represents to length of interest from the edge of the plate where the flow starts. Equations 4-8 are all localized Nusselts numbers, meaning that they are used when you are only interested in section of the plate length. If you are interested in the whole length of the plate equation 9 would be used. Equation nine is the average Nusselts number. To find the convective heat transfer coefficient the following equations would be used.
(Eq 10) $h_x = \frac{Nu_xk}{x}$
(Eq 11) $h_L = \frac{Nu_Lk}{L}$
In addition to laminar flow, there is also turbulent flow on a flat plate depending upon its length. As with laminar flow you will need to use Prandtl number for turbulent flow. However, you will also need to find the relationship between the fluids friction and the heat transfer. This is called Stanton number and is represented by the following equations. Just like Nusselts number the equation for Stanton number change as the Reynold number changes.
(Eq 12) $St_x = 0.332\frac{Re_x^{1/2}}{Pr^{2/3}} = \frac{c_{fx}}{2Pr^{2/3}}$
for Rex < 5 X 105
where cfx is the localized friction coefficient
(Eq 13) $St_X = 0.0296 \frac{Re_X^{-1/5}} {Pr^{2/3}} = \frac{c_{fx}}{2Pr^{2/3}}$
for 5 X 105 < Rex < 10 7
(Eq 14) $St_X = 0.185\frac{(logRe_X)^-2.584}{Pr^{2/3}} = \frac{c_{fx}}{2Pr^{2/3}}$
for 107 < Rex < 10 9
Equation 12 is the local Stanton number that represents laminar flow. Equations 13 and 14 are the local Stanton number that represent turbulent flow over the surface of a plate that is isothermal.
Finally to find the localized convective heat transfer coefficient using Stanton number the following equation would be used.
(Eq 15) $h_X = St_Xρc_pu_∞$
As mentioned earlier the fluid flow going over a long plate will normally start as laminar and then change to turbulent. There will be cases when you will want know the average convective heat transfer coefficient for the entire length of the plate. For situations like this the following Nusselts number would be used. Equation 11 would then be used to find the average convective heat transfer coefficient.
(Eq 16) $\overline{Nu}_L = Pr^{1/3}(0.037Re_L^{0.8} – 871)$
Restrictions: Tw=const, Rex <107, Recrit=5 X 105
The corresponding Stanton number for equation 16 is the following.
(Eq 17) $\overline{St} = \frac{0.037Re_L^{-0.2} – 871Re_L^{-1}}{Pr^{2/3}} = \frac{c_fL}{2Pr^{2/3}}$