We already know that all materials have a thermal resistance, but what about when you have two objects pressed up against each other, what would be the resulting contact resistance? Below is an example of a typical temperature profile when you have two objects contacting each other.
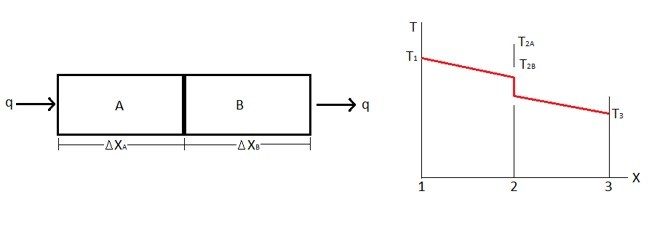
Notice that there is a sudden temperature drop at point 2 on the temperature graph. This is caused by the thermal contact resistance.
Thermal contact resistance is a product of the surface roughness of the two objects that are in contact with each other as well as a product of pressure. Generally thermal contact resistance is very difficult to predict accurately, and due to this fact it is generally not a good idea to have many different parts contacting each other if you are trying to remove heat from an object. Generally, if possible, it is best to have no contacting parts when trying to remove heat from a system, however this is normally not possible. Below is an image showing the surface contact between two objects.
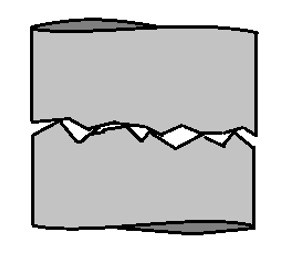
Notice the voids between the contacting parts. This is what causes high resistance to heat transfer. To help improve the contract resistance thermal paste could be used, or you could use something like Indium foil which helps fill in the voids between the two objects.
The mathematical approach to calculate thermal contact resistance is very straight forward, however you will need accurate data to plug into the variables. First let’s look at the general heat transfer equation that would represent the first image above.
(Eq 1) $q=k_AA\frac{T_1-T_{2A}}{Δx_A}=\frac{T_{2A}-T_{2B}}{1/h_cA}=k_BA\frac{T_{2B}-T_3}{Δx_B}$
Where hc is the contact coefficient.
Equation 1 can also be written as the following.
(Eq 2) $q=\frac{T_1-T_3}{Δx_A/k_AA+1/h_CA+Δx_B/k_BA}$
Mathematically the contact coefficient can be calculated using the following equation.
(Eq 3) $h_C=\frac{1}{L_g}\left(\frac{A_c}{A}\frac{2k_Ak_B}{K_A+k_B}+\frac{A_v}{A}k_f\right)$
Where, Ac is the contact area, Av is the void area, Lg is the thickness of the void, and kf is the thermal conductivity of the fluid that fills the void. What makes the thermal contact resistance so difficult to calculate is that it is very difficult to determine what the actual values for Ac, Av, and Lg are. Due to this fact, it is best to use reliable experimental data that will provide you with the contact coefficient. Below is data showing the contact coefficient for a few common materials.
μ-in |
(Celsius) |
(atm) |
m2C/W X 104 |
|
Ground Air |
||||
Ground Air |
||||
Ground Air |