Recall that convective heat transfer occurs when there is a fluid flowing over a body. To calculate the heat transfer rate the following equation would be used.
(Eq 1) $q = hA(T_w-T_∞)$
In the above equation h represents the convective heat transfer coefficient. To determine what this value is you will need to have an understanding of laminar and turbulent flow. Laminar flow occurs when there are distinct fluid layers through the boundary layer of the fluid. As the fluid velocity increases the flow will start to transition into turbulent flow. Once the flow is fully turbulent the fluid layers will no longer be observed and instead will become random. For heat transfer purposes turbulent flow will transfer heat better than laminar flow will.
In this section I will be talking about how to determine the heat transfer coefficient for tube flow. The first task is to determine whether the flow within the tube is laminar or turbulent; this will be determined using the Reynolds number. To calculate the Reynolds number for flow in a tube the following equation would be used.
(Eq 2) $Re_d = \frac{u_md}{ν}$
um = Average fluid velocity
d = Tube Diameter
ν=kinematic viscosity
When the Reynolds number is less than 2300 the flow will be laminar. The flow will start to transition from laminar to turbulent when the Reynolds number is between 2000 and 4000, and if the Reynolds number is greater than 4000 the flow will be turbulent. However, for greater accuracy of when the flow transitions from laminar to turbulent flow Moody’s Chart should be used, since this also takes in consideration the surface roughness of the tube walls.
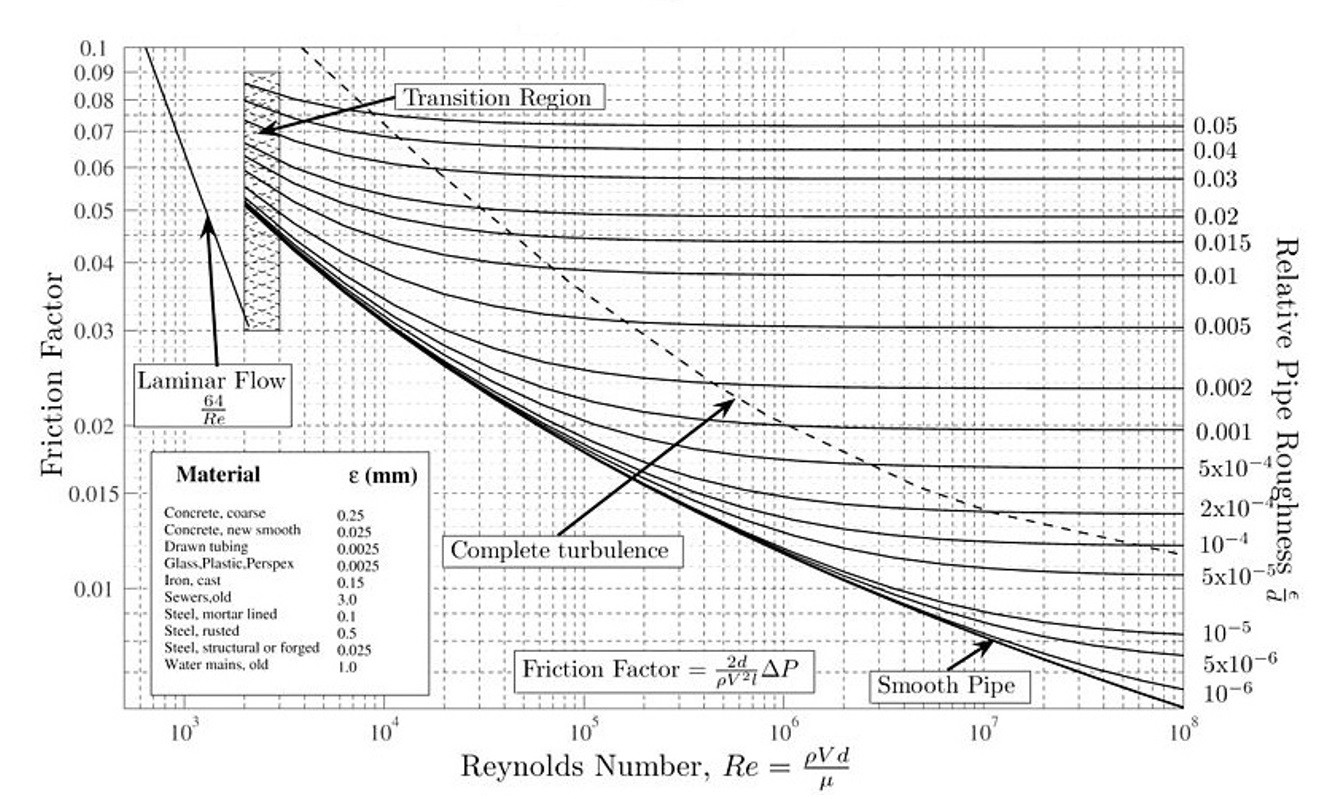
Currently all I have talked about is circular tubes. The above can also be applied to non-circular tubing. In order to do this you will need to find the hydraulic diameter of the non-circular tubing. This is done by using the following equation.
(Eq 3) $D_H = \frac{4A}{P}$
A = Cross-Sectional Area
P = Wetted Perimeter
Once the flow type is determined the convective heat transfer coefficient can be found using the following equation.
(Eq 4) $h = \frac{k}{d} Nu_d$
k = Thermal Conductivity of the Fluid
d = Tube Diameter
Nud = Nusselts Number
Below is a list of equations that can be used to calculate Nusselts number. Each equations has a set of restrictions that need to be met in order to use that particular equation to solve for the Nusselts number.
(Eq 5) $Nu_d = 0.023Re_d^{0.8}Pr^n$
Restrictions: Fully Developed Turbulent Flow
n = 0.4 for heating, n = 0.3 for cooling
2500 < Red < 1.25 X 105, 0.6 < Pr < 100
(Eq 6) $Nu_d = 0.0214 (Re_d^{0.8} – 100)Pr^0.4$
Restrictions: 104 < Red < 5 X 106
0.5 < Pr < 1.5
(Eq 7) $Nu_d = 0.012(Re_d^{0.87} – 280)Pr^{0.4}$
Restrictions: 3000 < Red < 106
1.5 < Pr < 500
(Eq 8) $Nu_d = 3.66 + \frac{0.0668(d/L)Re_dPr}{1 + 0.04[(d/L)Re_dPr]^{2/3}}$
Restrictions: Laminar Flow Tw = const
L = Full Length of Tube
For equations 5 – 8 Pr represents the Prandtl number of the fluid. To calculate Prandtl number the following equation would be used.
(Eq 9) $Pr = \frac{c_pμ}{k}$
Prandtl number can also be found in the Appendix of most Heat Transfer text books.