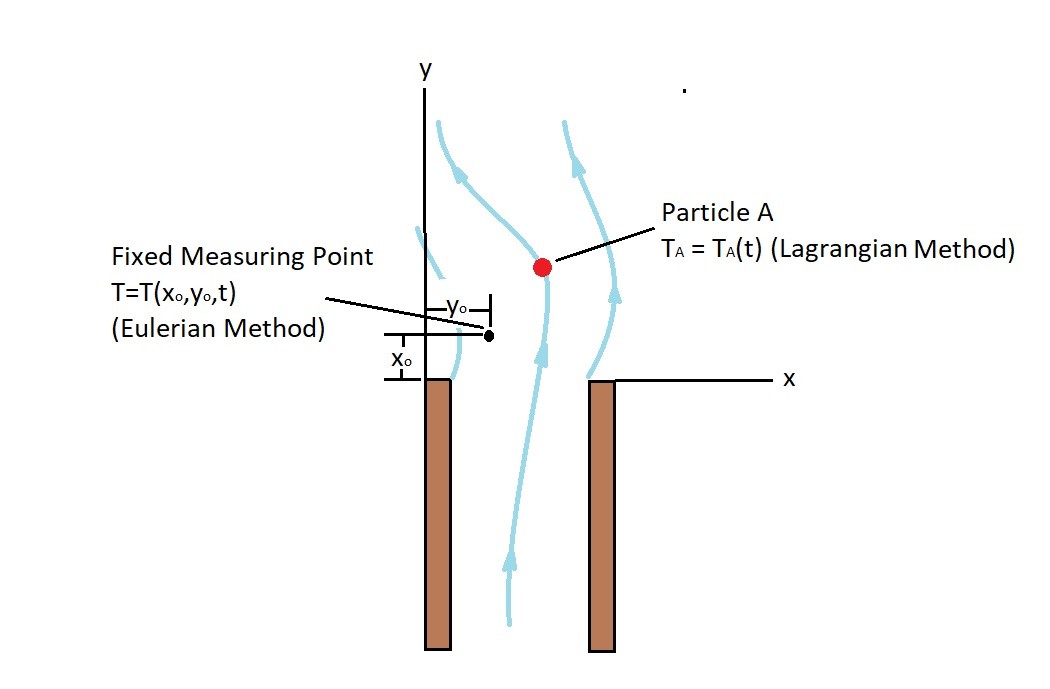
To analyze a fluid mechanics problem you can use two different methods. They are the Eulerian and Lagrangian Methods.
Eulerian Method
The Eulerian method analyzes the fluid field at specified points. This could be the velocity field, temperature field, pressure field, etc. What ever you are trying to analyze must be done at fixed points. By using multiple fixed points you will be able to determine what the fluid properties are as a function of time and space.
For example lets say you were analyzing the smoke coming out of a chimney. In order to analyze the smoke you will need to place a measuring device at different points within the chimney. You will than gather data at certain time intervals. As a result for an individual measuring device you will be able to determine how a specific property changes as a function of time for certain spacial coordinate. If you were interested in temperature that function would become the following
$T=T(x_o,y_o,z_o,t)$.
The spatial coordinates will remain the same, while only time can effect the temperature of the smoke. Since the measuring device must remained fixed, you will need to use multiple devices to determine how the temperature would change at different locations.
Lagrangian Method
Unlike the Eulerian method which analyzes fluid flow through a fixed point, the Lagrangian Method analyzes individual fluid particles. In other words a specific fluid particle will be “tagged”. After it is “tagged” the individual properties of the fluid particle can be determine as it moves as a function of time.
Let’s return to the chimney example from above. For the Eulerian method we had measuring devices at specific spatial locations. If we were to use the Lagrangian method we would need to attach a measuring device directly to the smoke particle to measure its temperature. As the smoke particle moves along it path the measuring device will measure the smoke particles temperature as a function of time. You can uses the following equation to describe the temperature of the fluid particle as a function of time.
$T_A = T_A(t)$