To common type of energy that a particle could have is potential and kinetic energy. Potential and kinetic energy are the exact opposite of each other. However, even though the two are the exact opposite of each other, they rely on each. This is because potential energy can create kinetic energy while kinetic energy can create potential energy.
Potential Energy
Potential energy represent the energy that particle already posses which could do work. This could be do to the objects position, current stresses that are within the object, or possibly an electrical charge.
Gravitational Potential Energy
One common form of potential energy is gravitational potential energy. Gravitational potential energy is dependent on the objects mass as well as distance between that object and another object such as the ground.
(Eq 1) $U_{1-2}=WΔy$
W = Weight
Δy = suspended height
U1-2 = Potential Energy
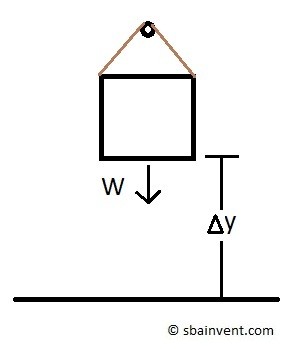
As seen in the image above as an object is hanging in space but has the potential to fall. It will have a potential energy that is the product of that objects weight and the distance the object is from the ground.
Example
A weight with a mass of 50kg is being held 2.5m above the ground. What amount of energy is stored in the object where the object has the potential to fall the full height and hit the ground?
Solution
$U_{1-2}=(9.81)(50)(2.5)=1.2~kJ$
Potential Energy and Springs
It is also possible to store energy in a spring when it forced out of its resting state. An example would be compressing a spring. Compressing a spring will store energy within the spring. Finally, when you remove the force holding the spring the stored energy will released as the spring returns to it resting position.
(Eq 2) $U_{1-2}=-\left( \frac{1}{2}ks_2^2-\frac{1}{2}ks_1^2 \right)$
k = spring constant
s2 = Initial spring length
s1 = New spring length
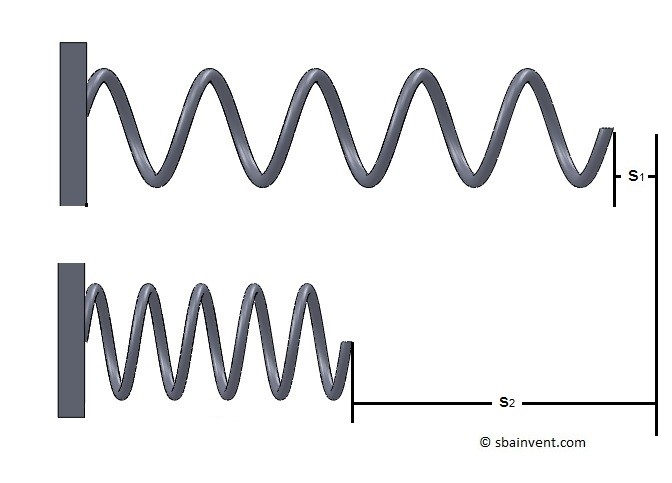
The variable k in equation 2 represents that spring constant, which represent the amount of deflection caused by a certain amount of force. Refer to equation 3.
(Eq 3) $k=\frac{f}{δ}$
f = force
δ = change in length
Example
A spring has a spring stiffness of 25$\frac{N}{mm}$. A force is deflecting the spring 20mm. How much energy is being stored in the spring?
Solution
$U_{1-2}=\frac{1}{2}(25)(20)^2=5~kJ$
Kinetic Energy
Kinetic energy is the energy of an object due to the motion of that object. As an object accelerates a certain amount of work is required for that object to reach its new velocity. The work will cause a change in kinetic energy stored within the object. While on the other if an object was to remain at a constant velocity than its stored kinetic energy would remain constant. Finally, in order for an object to come to a complete rest all of its kinetic energy would need to be expelled.
An particles kinetic energy is based off its velocity as well as its mass as seen in the equation below.
(Eq 4) $T=\frac{1}{2}mv^2$
m = Mass
v = velocity
T = Kinetic Energy
Example
A particle is traveling at a constant velocity of 15$\frac{m}{s}$. The particle than accelerates to a new velocity of 22$\frac{m}{s}$. The particles mass is 25kg. What was the change in the particles kinetic energy as it velocity changed from 15$\frac{m}{s}$ to 22$\frac{m}{s}$? What is the particles total kinetic energy as 22$\frac{m}{s}$?
Solution
Determine the particle’s kinetic energy at 22$\frac{m}{s}$.
$T_2=\frac{1}{2}(25)(22)^2= 6.1~kJ$
Determine the particles kinetic energy at 15$\frac{m}{s}$.
$T_1=\frac{1}{2}(25)(15)^2= 2.8~kJ$
Determine the change in kinetic energy due to the change in velocity.
$T_{1-2}=6.1-2.8=3.3~kJ$