Despite the fact that the ideal gas law is simple, its range of application is limited. As a result, additional equations of state have been developed. These equations were developed to represent $P-ν-T$ over a larger region without limitations. However, in order to accomplish this, these equations had to become more complicated. The equations that will be discussed are the Van der Waals equation, Beattie-Bridgeman equation, Benedict-Webb-Rubin Equation, and Virial Equation.
Van der Waals Equation Equation of State
The Van der Waals equation is one of the first attempts on determining the behavior of a substance accurately. It does this by using two constants that are derived from the behavior of the substance at its critical point. Refer to the equation below.
(Eq 1) $\left(P+\frac{a}{ν^2}\right)(ν-b)=RT$
$P$ =absolute pressure
$ν$ = specific volume
$T$ = absolute temperature
$R$ = gas constant
This equation was designed to improve the ideal gas equation by considering the intermolecular attraction forces, as well as the volume occupied by the molecules themselves. The term $a/ν^2$ in equation 1 accounts for the intermolecular forces. In addition, $b$ accounts for the volume occupied by the gas molecules.
In order to make this equation work, the constants $a$ and $b$ need to be determined. This is done by making the observation that the critical isotherm on the P-ν diagram has a horizontal inflection point at the critical point.
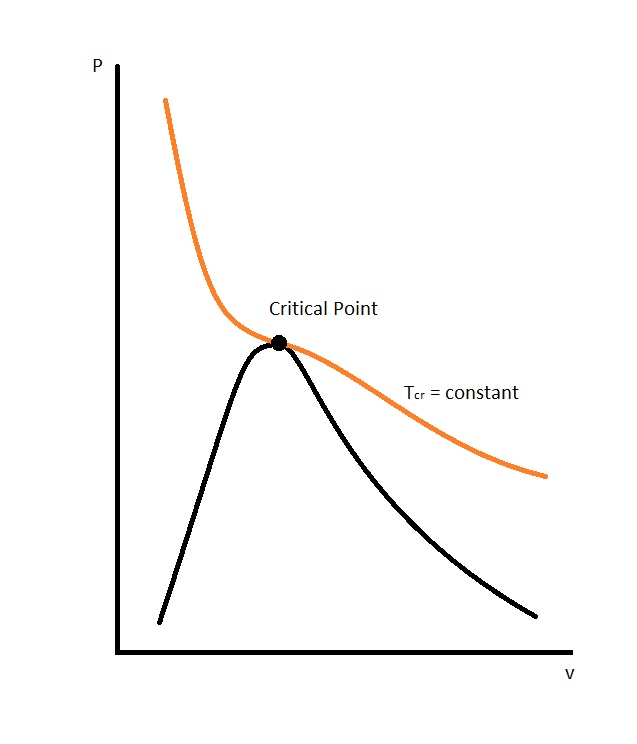
As a result, we will be able to conclude that the first and second derivative of P in respect to ν will be zero at the critical point. In turn, the following equations to determine the constants $a$ and $b$ can be derived using the following equations.
(Eq 2) $a=\frac{27R^2T^2_{cr}}{64P_{cr}}$
(Eq 3) $b=\frac{RT_{cr}}{8P_{cr}}$
Generally, the accuracy of the van der Waals equation is questionable. However, it can be improved by deriving the values for the constants a and b over a wider range instead of a single point.
Beattie-Bridgeman Equation of State
The next equation of state that we are going to look at is called the Beattie-Bridgeman Equation. This equation was developed in 1928. It is based of off 5 constants that are determine experimentally. Refer to the equation below.
(Eq 2) $P=\frac{R_uT}{\bar{ν}^2}\left(1-\frac{c}{\bar{ν}T^3}\right)(\bar{ν}+B)-\frac{A}{\bar{ν}^2}$
where,
$A=A_o\left(1-\frac{a}{\bar{ν}}\right)$
$B=B_o\left(1-\frac{b}{\bar{ν}}\right)$
This equation is reasonably accurate up to densities that are $0.8ρ_{cr}$ of the substance. Finally, the table below can be used to fill in the constants for certain gases.
|
Gas |
$A_o$ |
$a$ |
$B_o$ |
$b$ |
$c$ |
|
Air |
$131.8$ |
$0.01931$ |
$0.04611$ |
$-0.001101$ |
$4.34 × 10^4$ |
|
Argon |
$130.8$ |
$0.02328$ |
$0.03931$ |
$0.0$ |
$5.99 × 10^4$ |
|
Carbon dioxide |
$507.3$ |
$0.07132$ |
$0.10476$ |
$0.07235$ |
$6.60 × 10^5$ |
|
Helium |
$2.189$ |
$0.05984$ |
$0.01400$ |
$0.0$ |
$40$ |
|
Hydrogen |
$20.01$ |
$-0.00506$ |
$0.02096$ |
$-0.04359$ |
$504$ |
|
Nitrogen |
$136.2$ |
$0.02617$ |
$0.05046$ |
$-0.06910$ |
$4.20 × 10^4$ |
|
Oxygen |
$151.1$ |
$0.02562$ |
$0.04624$ |
$0.004208$ |
$4.80 × 10^4$ |
Benedict-Webb-Rubin Equation of State
To further the Beattie-Bridgeman Equation, Benedict, Webb, and Rubin extended it to increase its accuracy. In order to do this they had to raise the number of constants to eight. In turn, this resulted in the following equation.
(Eq 3) $P=\frac{R_uT}{\bar{ν}}$$+\left(B_oR_uT-A_o-\frac{C_o}{T^2}\right)\frac{1}{\bar{ν}^2}$$+\frac{bR_uT-a}{\bar{ν}^3}$$+\frac{aα}{\bar{ν}^6}$$+\frac{c}{\bar{ν}^3T^2}\left(1+\frac{γ}{\bar{ν}^2}\right)e^{-γ/\bar{ν}^2}$
Due to the added constants, the accuracy of the equation has increased to $2.5ρ_{cr}$ of the substance.
| Gas | $a$ | $A_o$ | $b$ | $B_o$ | $c$ | $C_o$ | $α$ | $γ$ |
| n-Butane | $190.7$ | $1022$ | $0.039998$ | $0.12436$ | $3.205×10^7$ | $1.006×10^8$ | $1.101×10^{-3}$ | $0.0340$ |
| Carbon dioxide | $13.86$ | $277.3$ | $0.00721$ | $0.04991$ | $1.511×10^6$ | $1.404×10^7$ | $8.470×10^{-5}$ | $0.00539$ |
| Carbon monoxide | $3.71$ | $135.9$ | $0.002632$ | $0.05454$ | $1.054×10^5$ | $8.673×10^5$ | $1.350×10^{-4}$ | $0.0060$ |
| Methane | $5.00$ | $187.9$ | $0.003380$ | $0.04260$ | $2.578×10^5$ | $2.286×10^6$ | $1.244×10^{-4}$ | $0.0060$ |
| Nitrogen | $2.54$ | $106.7$ | $0.002328$ | $0.04074$ | $7.379×10^4$ | $8.164×10^5$ | $1.272×10^{-4}$ | $0.0053$ |
Virial Equation of State
The final equation of state that will be discussed is the Virial Equation of state. Unlike the previous equation of states, the virial equation of state is expressed in a series form. As a result, the accuracy of the equation is dependent on the number of terms used. Refer to the following equation.
(Eq 4) $P=\frac{RT}{ν}+\frac{a(T)}{ν^2}+\frac{b(T)}{ν^3}+\frac{c(T)}{ν^4}+\frac{d(T)}{ν^5}…$
The coefficients $a(T)$, $b(T)$, $c(T)$, etc within this equation are functions of temperature. In turn, these coefficients are referred to as virial coefficients. To determine the coefficients you will need to rely on experimental data. However, you can also use a theoretical analysis to determine these coefficients.