Steady-flow devices operate under the same conditions for a long period of time after the initial transient start up period. Examples of these types of devices are turbines, compressors, and nozzles. In turn, the process of these devices can be represented by an ideal process called a steady-flow process. A steady flow process is defined as “a process during which a fluid flows through a control volume steadily.” This means that even though a fluid property can change from one point to another they will remain constant during the entire process.
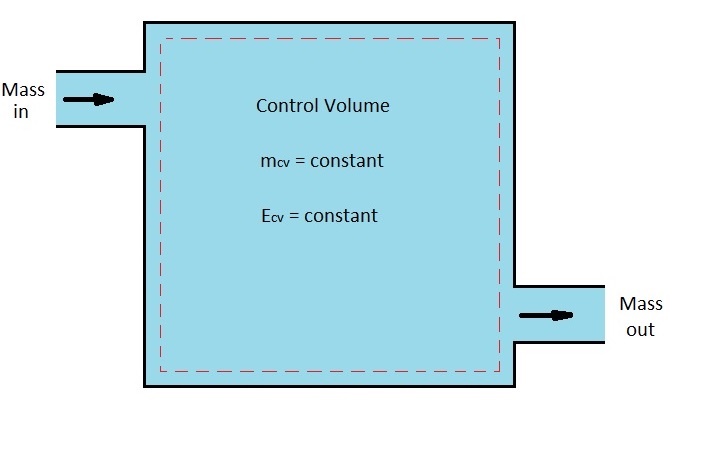
As a steady-flow process occurs, neither intensive or extensive properties will change with time. As a result, properties like volume, mass, and energy will remain constant. In turn, the boundary work will be zero during the process. in addition, the mass or energy entering the control volume must be equal to the mass or energy the is leaving.
Mass Flow
As stated above the fluid properties at the inlet or exit must remain constant. However, these properties can be different at different inlets and outlets. In addition, they can also vary over the cross-sectional area of an inlet or outlet. But for the the process to be considered a steady-flow process all properties must be constant at the inlet or outlet. In turn, this will result in the following mass balance.
(Eq 1) $\sum{_{in}}\dot{m}=\sum{_{out}}\dot{m}$
If the control volume had one inlet and one outlet equation 1 would become the following.
(Eq 2) $\dot{m}_1=\dot{m}_2$
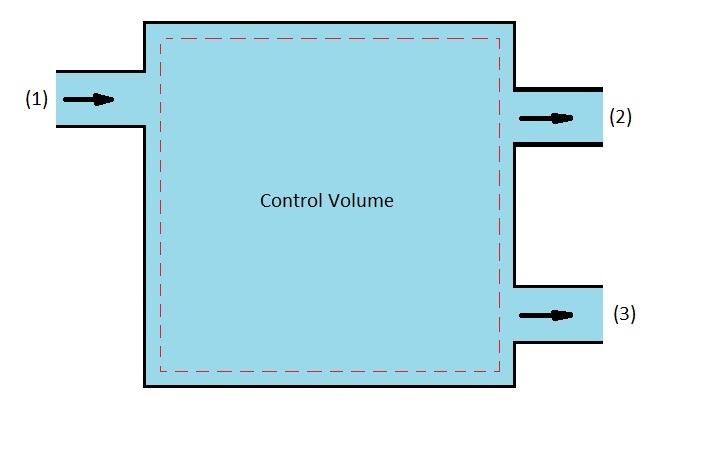
On the other hand, if there was one inlet but two outlets than the following mass balance equation would result.
(Eq 3) $\dot{m}_1 = \dot{m}_2+\dot{m}_3$
Steady Flow Process: Energy
As with mass, the energy that enters a control volume during a steady flow process must be equal to the energy that leaves. As a result, the total energy content inside of the control volume will remain constant, $ΔE_{CV}=~constant$. In turn, the change in total energy will be zero, $ΔE_{CV}=o$. This will result in the following energy balance equation.
(Eq 4) $\dot{E}_{in}=\dot{E}_{out}$
Due to the fact that energy can be transferred by heat, work, and mass, equation 4 can be expanded to the following equation.
(Eq 5) $\dot{Q}_{in}+\dot{W}_{in}+\sum{_{in}}\dot{m} =\dot{Q}_{out}+\dot{W}_{out}+\sum{_{out}}\dot{m}θ$
or
(Eq 6) $\dot{Q}_{in}+\dot{W}_{in}+\sum{_{in}}\dot{m}\left(h+\frac{v^2}{2}+gz\right)=$$\dot{Q}_{out}+\dot{W}_{out}+\sum{_{out}}\dot{m}\left(h+\frac{v^2}{2}+gz\right)$
$\dot{Q}$ = heat
$\dot{W}$ = work
$h$ = enthalpy
$v$ = fluid velocity
$g$ = gravitational acceleration
$z$ = elevation
The energy balance given in these equations is intuitive when the direction and magnitude of heat and work is known. However, during a general analytical study it is possible you will not know how the heat and work interact. When this is the case it is common practice to assume heat transfers into the system while work is produced by the system. After solving the problem, if you obtain a negative value than the opposite of the above assumption is true. If you do apply this assumption than the first-law of energy balance relation becomes the following.
(Eq 7) $\dot{Q}-\dot{W}=\sum{_{out}}\dot{m}\left(h+\frac{v^2}{2}+gz\right)$$-\sum{_{in}}\dot{m}\left(h+\frac{v^2}{2}+gz\right)$
For single-stream devices equation 7 becomes the following.
(Eq 8) $\dot{Q}-\dot{W}=\dot{m}\left[h_2-h_1+\frac{v^2_2-v^2_1}{2}+g(z_2-z_1)\right]$
Finally, if you need to know the energy balance per unit-mass balance than you would divide the above equations by $\dot{m}$. Below is the unit-mass balance after dividing equation 8 by $\dot{m}$.
(Eq 9) $q-w=h_2-h_1+\frac{v^2_2-v^2_1}{2}+g(z_2-z_1)$