Even though the ideal gas equation is a simple convenient equation to use, it is not always accurate. To be more specific, at the saturation region, as well as the critical point, the behavior of a gas will significantly deviate from an ideal gas. To compensate for this deviation, a correction factor is used. This is known as the compressibility factor,$Z$.
Compressibility Factor
To determine the compressibility factor the following equation is used.
(Eq 1) $Z=\frac{Pν}{RT}$
$P$ = absolute pressure
$ν$ = specific volume
$T$ = absolute temperature
$R$ = ideal gas constant
In addition, the compressibility factor can expressed by the following equation.
(Eq 2) $Z=\frac{ν_{actual}}{ν_{ideal}}$
If the gas is ideal, than the compressibility factor will be $Z=1$. However, for a real gas it can can be greater or less than unity. In addition, the further $Z$ is from unity the more the gas will deviate from an ideal gas behavior.
Temperature and Pressure
Generally a real gas will most closely resemble an ideal gas when the pressure is low, or the temperature is high. However, what would actually be considered a sufficiently low pressure or high temperature is dependent on the pure substance in question. For example, at $-100^oC$ air at atmospheric pressure can still be considered an ideal gas. Instead what determines if a substance can be considered an ideal gas is the ratio of the current pressure over the critical pressure in comparison to the ratio of the current temperature over the critical temperature. The results of the ratios are known as the reduced pressure and reduced temperature.
(Eq 3) $P_r=\frac{P}{P_{cr}}$
(Eq 4) $T_r=\frac{T}{T_{cr}}$
In turn, the reduced pressure and temperature can be used to approximate the compressibility factor of all gases. This is also known as the principle of corresponding states. The principle of corresponding states allow us to obtain the generalized compressibility chart which is used to determine $Z$ for a real gas.
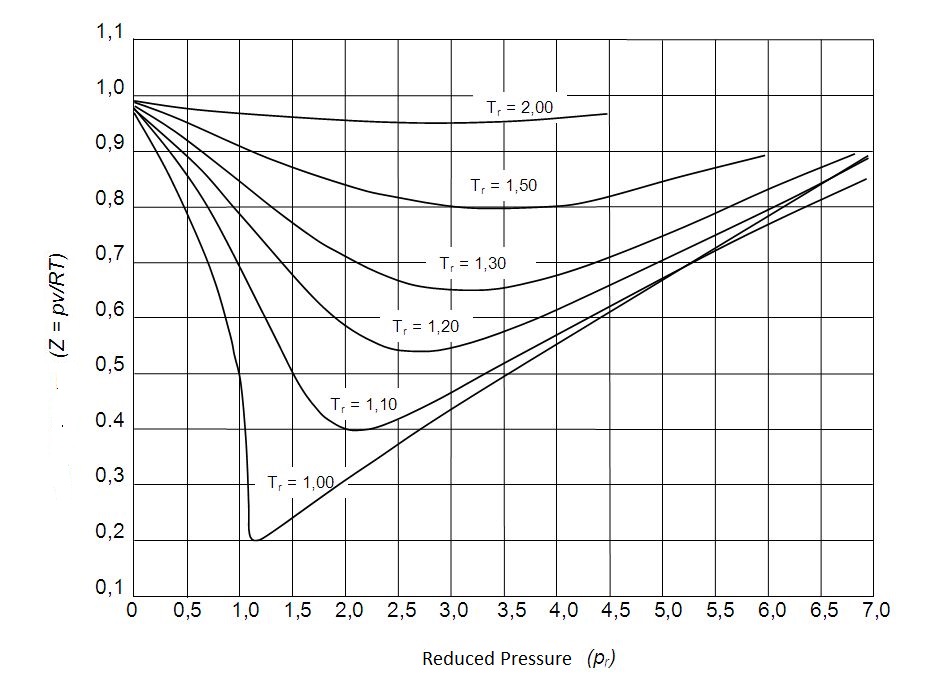
The following observation can be concluded from the generalized compressibility chart.
- At a very low pressure a gas will behave as an ideal gas regardless of what the temperature is.
- At a significantly high temperature a gas will behave like an ideal gas regardless of pressure.
- The deviation of a gas from an ideal gas will be greatest at the critical point.
Finally, there can be cases when you know what P and ν or T and ν are instead of P and T. When this is the case you can still use the generalized compressibility chart. However, to do this you would need to determine the third property. This can be done through trial and error, or you can define a reduced property called the pseudo-reduced specific volume.
(Eq 5) $ν_r=\frac{ν_{actual}}{RT_{cr}/P_{cr}}$