Commonly the ideal gas is defined by $Pν=RT$. In this equation $P$ is the absolute pressure, $ν$ is specific volume, $R$ is the gas constant, and $T$ is the absolute temperature. However, internal energy and enthalpy can also be related to the ideal gas law.
Internal Energy Ideal Gas
First, let’s discuss internal energy. To determine the internal energy of an ideal gas you would use the following equation.
(Eq 1) $u=u(T)$
Equation one shows that the internal energy of an ideal gas is a function of the temperature only. Joule showed this through experimentation. He did this by submerging two tanks in water that were connected with a pipe and valve. One tank contained air at a high pressure. The other was completely evacuated. After thermal equilibrium was obtained, the valve was opened to allow air to to pass from the high pressure tank into the evacuated tank. During this process he noticed that the temperature of water bath did not change. As a result, he reasoned that the internal energy is only a function of temperature and is not effected by pressure or specific volume. However, this is only true for ideal gases. For a real gas that differs significantly from an ideal gas, internal energy is not a function of internal energy alone.
Enthalpy Ideal Gas
Enthalpy is a thermodynamic property that represents the systems internal energy plus the product of the systems pressure and volume. In other words, it represents the total heat content of a system. For an ideal gas, the definition of enthalpy and the equation of state is as follows.
(Eq 2) $h=u+RT=\cases{h=u+Pν \cr Pν=RT}$
However, since $R$ is constant, and $u=u(T)$, for an ideal gas enthalpy will also be a function of temperature only.
(Eq 3) $h=h(T)$
Specific Heat Ideal Gas
Due to the fact that both enthalpy and internal energy are solely dependent on temperature, the specific heat of an ideal gas is also only temperature dependent. As a result, the the internal energy and enthalpy of an ideal gas can be expressed using the following.
(Eq 4) $du=c_v(T)dt$
$c_v$ = specific heat at a constant volume
(Eq 5) $dh=c_p(T)dT$
$c_p$ = specific heat at a constant pressure
In order to determine the change in internal energy or enthalpy for a process you would integrate equations 4 and 5.
(Eq 6) $Δu=u_2-u_1=\int{}^2_1~c_v(T)dt$ (kJ/kg)
and
(Eq 7) $Δh=h_2-h_1=\int{}^2_1~c_p(T)dt$ (kJ/kg)
To solve these equations we will need to find a relation for $c_v$ and $c_p$ as a function of temperature. To do this you can use data that is based off of direct measurement or calculations from statistical behavior of molecules. Below is a table showing the specific heat of air at various temperatures.
|
Air |
|||
|
Temperature (K) |
$c_p$ (kJ/kg-K) |
$c_v$ (kJ/kg-K) |
k |
|
250 |
1.003 |
0.716 |
1.401 |
|
300 |
1.005 |
0.718 |
1.400 |
|
350 |
1.008 |
0.721 |
1.398 |
|
400 |
1.013 |
0.726 |
1.395 |
|
450 |
1.020 |
0.733 |
1.391 |
|
500 |
1.029 |
0.742 |
1.387 |
|
550 |
1.040 |
.753 |
1.381 |
|
600 |
1.051 |
.764 |
1.376 |
|
650 |
1.063 |
.776 |
1.370 |
|
700 |
1.075 |
.788 |
1.364 |
|
750 |
1.087 |
0.800 |
1.359 |
|
800 |
1.099 |
0.812 |
1.354 |
|
900 |
1.121 |
0.834 |
1.344 |
|
1000 |
1.142 |
0.855 |
1.336 |
In addition, over small temperatures changes, such as a few hundred degrees or less, the specific heat can be approximated as linear. As a result, the specific heat function in equations 6 and 7 can be replaced with a constant average. This would yield the following equations.
(Eq 8) $u_2-u_1=c_{v,avg}(T_2-T_1)$
(Eq 9) $h_2-h_1=c_{p,avg}(T_2-T_1)$
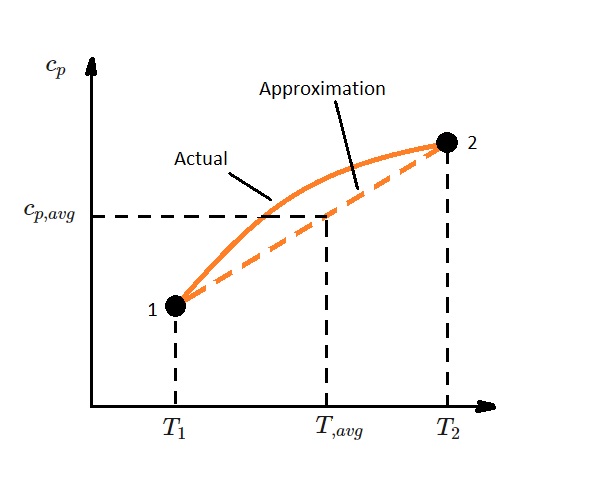
Specific Heat Relations for an Ideal Gas
For an ideal gas there is a special relationship between $c_p$ and $c_v$. This is found by differentiating the relation $h=u+RT$. In turn, this will yield $dh=du+Rdt$. Next, $dh$ is replaced with $cpdT$ and $du$ is replaced with $c_vdT$. Then after dividing the resulting equation by $dT$ we will obtain the following equation.
(Eq 10) $c_p=c_v+R$
This equation will give us the ability to determine $c_v$ when we have knowledge of $c_p$ and the gas constant $R$. In turn, we can now introduce another ideal-gas property called the specific heat ratio $k$. The specific heat ratio is defined using the following equation.
(Eq 11) $k=\frac{c_p}{c_v}$