Recall a closed system is a system that has a solid boundary layer so that mass cannot enter or leave the system, but energy can transfer across the boundary layer. There can be two different types of closed systems, a closed system that has the boundary layer fixed on all sides, and a closed system that has a moving boundary; refer to the figure below.

For this section I’m going to discuss how to calculate the work required to move the moving boundary in the figure above.

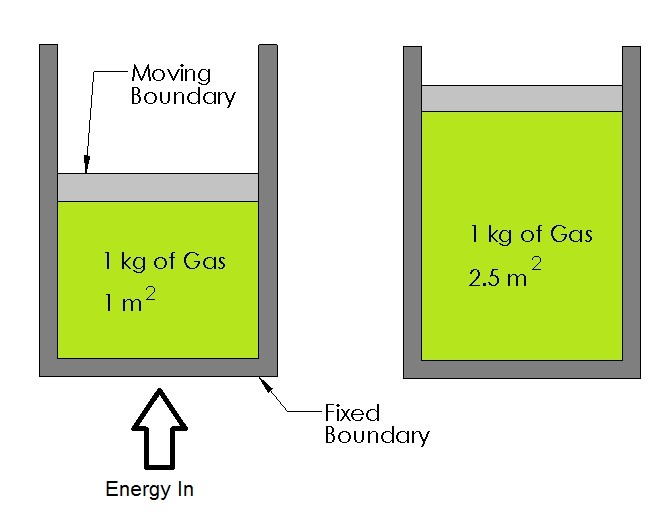
Moving Boundary Work

In this section I will show how to calculate the amount of energy going to into a system, such as a cylinder, that is required to make that system expand or contract resulting in mechanical work. An example of this in real life would be the cylinders inside a car’s engine expanding due to the explosions caused by the spark plugs.

Recall the fundamental method of calculating work is by multiplying the distance an object traveled due to a force that was applied by to the object. Refer to the equation below.

(Eq 1)   $W=F∫ds=FΔs$

Now when dealing with something like a cylinder the work is done by pressure change that would cause the volume inside the cylinder to change moving a piston. To calculate this equation 1 would have to be modified. Refer to equation 2.

(Eq 2)  $W=P∫dV=PΔV$

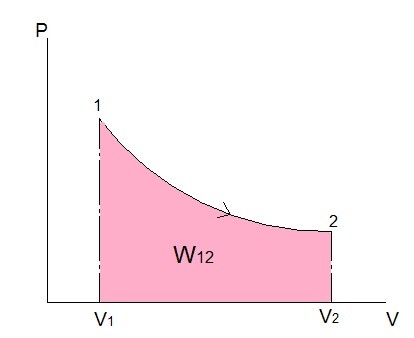
Notice that for both equations 1 and 2 I showed the calculation of work as an integral due to a distance change or volume changed multiplied by a force or pressure. By using an integral, the area under the process curve is found, and this area represents the boundary work. Refer to the figure below.

As I’ve stated above, the above image represents the work for a process. However, in most cases you want this process to repeat which means another process has to occur to result in a complete cycle. To return a piston inside a cylinder back to its original position a certain amount of work is required. The difference between the work for the two processes will result in a net work. Refer to the equation and figure below.

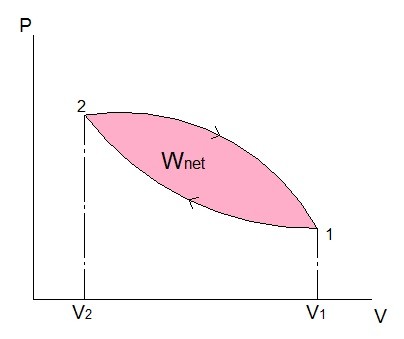
(Eq 3)  $W_{net}=W_{21}-W_{12}$

Finally, the above equation 2 assumes that the system a state of quasi-equilibrium throughout the process. For this to happen the process has to occur at a slow pace, which means for most real life situation equation 2 will only provide rough estimates of the true work required to move the piston inside of a cylinder. To calculate the true boundary work tests would have to be conducted on the system so that measurements can be obtained.

Energy Balance for Close Systems

From the first law of thermodynamics, energy cannot be created or destroyed. This means that net energy coming in to the system minus the net energy coming out the system, whether the energy coming in or out is due to heat, work, or mass, will result in a change of the internal energy, kinetic energy, or potential energy of the system. Refer to the equation below.

(Eq 4)  $E_{in}-E_{out}=ΔE_{system}$

From the above equation, the amount of heat going into the system to cause work can be calculated. Refer to the equation below.

(Eq 5)   $Q-W=ΔE$

$Q$ = Heat Energy

$W$ = Work Energy

$E$ = System Energy

Note equation 5 assumes that heat and work are not different from one another due to the first law of thermodynamics. However, from later sections you will learn that there is a difference between heat and work because of the second law of thermodynamics.