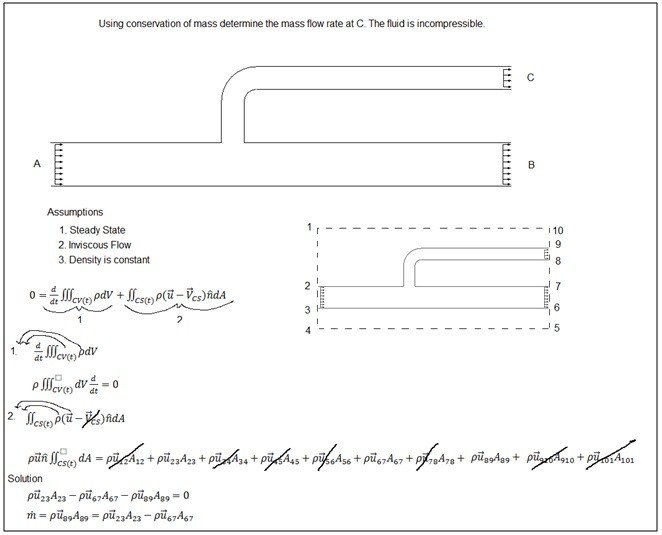
Conservation of mass is one of the fundamental laws of fluid mechanics and is applied in almost every fluid mechanics problem whether you realize it or not. Conservation of mass takes in consideration that mass cannot be created or destroyed. This means what goes in must come out. The general equation for conservation of mass can be seen below.
(Eq 1) $0=\frac{d}{dt}\iiint_{CV(t)}ρdV+\iint_{CS(t)}ρ(\vec{u}-\vec{V}_{CS})\hat{n}dA$
Equation 1 can be broken into two general parts that will change depending on the type of problem it is. These are the mass collection in the control volume (CV) which is represent by equation 2 and the second part is the mass flux through the control surface (CS).
(Eq 2) $\frac{d}{dt}\iiint_{CV(t)}ρdV$
(Eq 3) $\iint_{CS(t)}ρ(\vec{u}-\vec{V}_{CS})\hat{n}dA$
In equation 2 there are two properties that need to be considered. They are density and volume. First let’s talk about density. Notice that there is an integral in respect to volume and a derivative in respect to time. When considering density for this part of the equation you need to look at the problem and first say is the density the same in all parts of the CV or is it different. If it is same you can move the density symbol out of the integral. Refer to equation 4.
(Eq 4) $\frac{d}{dt}ρ\iiint_{CV(t)}dV$
Now the next thing you need to consider is whether the density changes in respect to time, or does it remain constant. In other words is the fluid compressible or incompressible. If the density does not change with respect to time it can be moved out of the derivative, refer to equation 5.
(Eq 5) $ρ\frac{d}{dt}\iiint_{CV(t)}dV$
Next how the control volume reacts in respect to time needs to be determined. If it does then it must remain within the derivative, but if it doesn’t then in can be removed from the derivative which in that case the equation can be modified, refer to equation 6.
(Eq 6) $\iiint_{CV(t)}dVρ\frac{d}{dt}$
Finally, if the volume does not change with respect to time, and the density does not change in respect to time and is constant throughout the CV , this part of the conservation of mass equation can be removed.
The second part of the conservation of mass equation represent by equation 3 takes in consideration of mass entering and leaving the control volume through a control surface. In this part of the equation the velocity of the flow needs to be taken into consideration as well as the density. However, notice that there is only an integral in respect to the area of the control surface that needs to be considered. So if the density is constant across the control surface then it can be removed from the integral, refer to equation 7.
(Eq 7) $ρ\iint_{CS(t)}(\vec{u}-\vec{V}_{CS})\hat{n}dA$
Next, if the velocity does not change in respect to the control surface then it can be removed from the integral, refer to equation 8.
(Eq 8) $ρ(\vec{u}-\vec{V}_{CS})\hat{n}\iint_{CS(t)}dA$
An example of when velocity cannot be removed from the integral is when viscous forces are in effect and a boundary layer develops.
Finally, if the control system is stationary then the velocity that represents it will go to zero and can be removed from the equation, refer to equation 9.
(Eq 9) $ρ\vec{u}\hat{n}\iint_{CS(t)}dA$