Piping and pump systems that are in parallel will have a different effect on flow rate and pressure then piping systems that are in series. In either case, the continuity equation and Bernoulli’s equation can be used to describe the change in pressure or flow rate.
Pipes & Pumps in Series
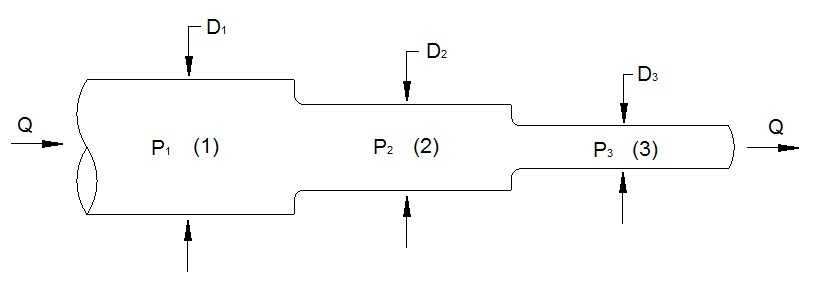
Piping that is in series will experience pressure losses while the fluids flow rate should theoretically be the same throughout the piping system. We already know by using Bernoulli’s equation and the continuity equation that a pressure change will occur when a fluid goes through a pipe that has a change in cross-sectional area. In addition to this, there could be cases where there is a resistance to the fluid flow due to a valve that was partially closed or possibly build up on a pipe. Elbows and turns in a pipe can also cause a pressure loss. All of these losses will sum up to a total loss for a pipe that is in series. Refer to equation 1.
(Eq 1) $dP=dP_1+dP_2···dP_n$
P = Pressure
Identical Pumps in Series
Identical pumps in series will behave the same way as pipes in series, except instead of dealing with a pressure loss, an increase in pressure head will result while the flow will remain the same since the pumps will be pulling or pushing fluid from the same source. Refer to equation 2.
(Eq 2) $P_T=P_1+P_2···P_n$
Pipes & Pumps in Parallel
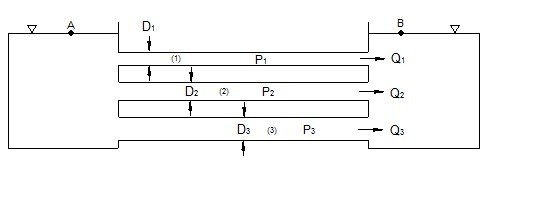
Pipes that are in parallel will experience the same pressure loss across each pipe. In addition, each pipe will experience a different flowrate of fluid going through it. Refer to equation 3 to calculate the different flow rates in each pipe when the same type of fluid is flowing through each pipe.
(Eq 3) $Q=Q_1+Q_2···Q_n$
Q = Flow Rate
Equation 3 is only for a pipe system that is in parallel that has the same fluid flowing through each pipe. However, there can be cases when the fluid flowing through each pipe is not the same. When this happens, the mass flow rate of the fluid should be used since it also considers the density of the fluid. Refer to equation 4.
(Eq 4) $\dot{m}=ρ_1Q_1+ρ_2Q_2···ρ_nQ_n$
ρ = Density
Identical Pumps in Parallel
Identical pumps that are in parallel behave the same as pipes that are in parallel. They will increase the fluids flow rate by the number of identical pumps that are in parallel while the pressure head will remain the same. Refer to equation 5.
(Eq 5) $Q_T=Q_1+Q_2···Q_n$