The basic radiation heat transfer equation below considers the total radiative heat transfer from one body to another if all of the emitted radiation from both body come in contact with the other body and then is absorbed by the other body instead of being reflected back. This is the simplest way to calculate radiative heat transfer. It is also the maximum amount of radiative heat transfer that can occur between two bodies.
(Eq 1) $E_{b1}A_1=E_{b2}A_2$
Now in reality some of the thermal radiation coming off an object will strike another object while some of it will most likely miss the object completely. There are also cases where the thermal radiation that missed the object could have a portion of that energy reflected off a third surface and then strike the object that it had original missed, or possibly strike the object that had emitted the radiation to start with. Refer to the image below.
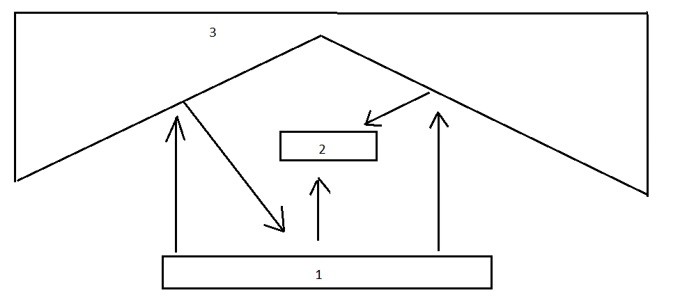
From the above image it can be seen that trying to predict the amount of thermal radiation that will strike an object can become complicated fairly fast, especially if you start considering grey bodies. However, for right now let’s assume that everything is a blackbody. Which is this case equation 1 would be modified to the following.
(Eq 2) $E_{b1}A_1F_{12}=E_{b2}A_1F_{21}$
In the above equation, F represents the radiation shape factor between the two surfaces of interest.
In order to determine the shape factor the following equation can be used.
(Eq 3) $q_{net1-2} = (E_{b1}-E_{b2})∫_{A2}∫_{A1}cosΦ_1cosΦ_2\frac{dA_1dA_2}{πr^2}$
You can also use the shape factor graphs that can be found in most heat transfer textbooks. Below are graphs that can be used for two perpendicular rectangles with a common edge, two coaxial cylinders, and two parallel equal rectangles.
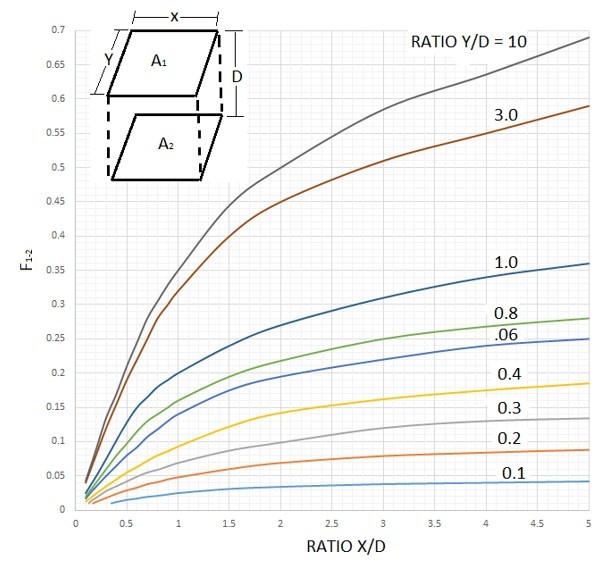
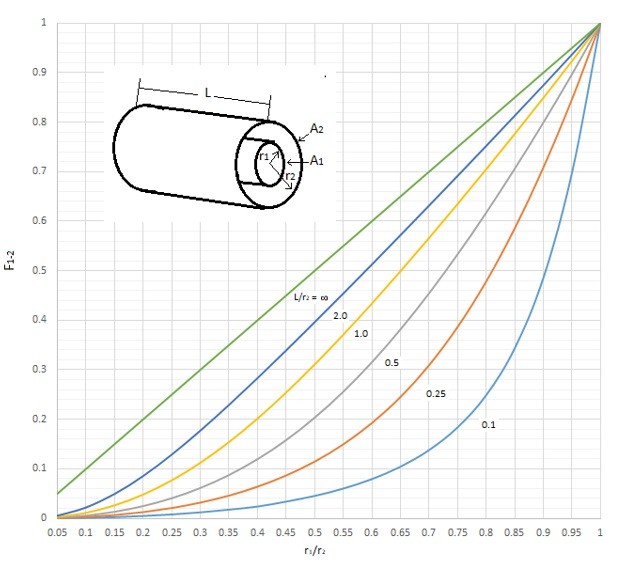
Finally, once the shape factor is determined, the following equation can be used to determine the total heat transfer between two black bodies.
(Eq 4) $q=σA_1F_{12}(T_1^4-T_2^4)$
Example
There are two parallel plates that are spaced .2 meters apart. They both have a length of 2m and a width of 1m. One plate is set at 400 degrees Celsius and the other has a temperature of 700 degrees Celsius. What is the total heat transfer between the two plates?
First, we need to determine the radiation shape factor of the two plates. This can be determine by using the shape factor graph for two equal parallel rectangles.
$\frac{Y}{D}=\frac{2}{.2}=10$, $\frac{X}{D}=\frac{1}{.2}=5$, $F_{12}=.69$
The heat transfer for thermal radiation can now be determined using equation 4. Remember that temperature has to be converted to Kelvin.
$q=(5.669X10^-8)(2)(.69)(973^4-673^4)=54kW$
Relationship between Shape Factors
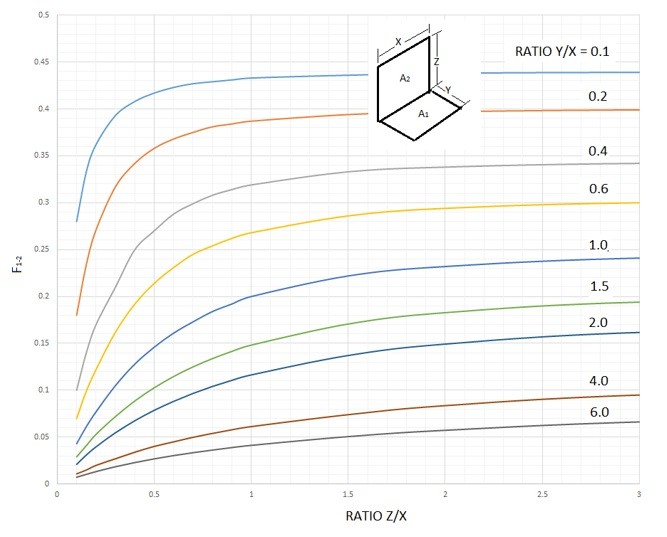
There could also be cases where you are interested in the heat transfer on a specific surface that you won’t be able to find the shape factor directly from the shape factors seen in the graphs above. An example of this is the image below.
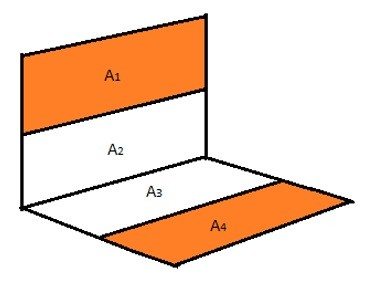
In the above image we are looking for the shape factor between A1 and A2. Currently we don’t have any data available to find the shape factor directly. However we do have data to find the shape factor between to perpendicular rectangles that share a common edge. This can be seen in the image below.
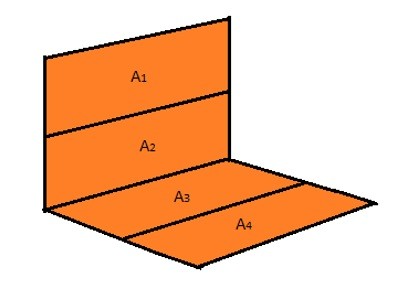
The resulting equation for the shape factor of the image above would be the following:
(Eq 5) $A_{1,2}F_{1,2-3,4}=A_1F_{1-3,4}+A_2F_{2-3,4}$
From the above equation it can be seen there are two additional unknowns that we now need to find additional shape factor relationships for. F2-3,4 can be found using the graph for perpendicular rectangle that share the same edge. F1-3,4 however does not share an edge. This can be seen in the image below and the shape factor equation is represented by equation 6.
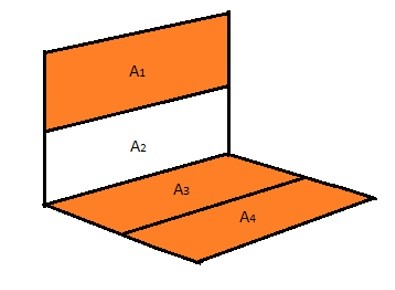
(Eq 6) $A_1F_{1-3,4}=A_1F_{1-3}+A_1F_{1-4}$
Due to the fact that neither F1-3 nor F1-4 share a common edge an additional equation needs to be used to solve for all of the unknowns. This can be seen in the image below and is represented by equation 7.
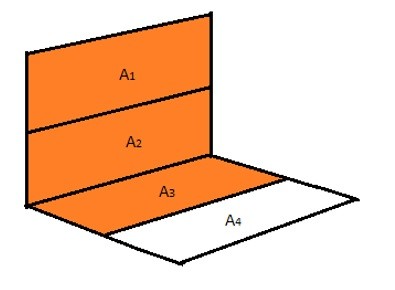
(Eq 7) $A_{1,2}F_{1,2-3}=A_1F_{1-3}+A_2F_{2-3}$
Next, solve equation 7 for A1F1-3.
(Eq 8) $A_1F_{1-3} = A_{1,2}F_{1,2-3}-A_2F_{2-3}$
Equation 8 and can now be implemented into equation 6 which will result in the equation below.
(Eq 9) $A_1F_{1-3.4} = A_{1,2}F_{1,2-3}-A_2F_{2-3}+A_1F_{1-4}$
Next, insert equation 9 into equation 5 as seen below.
(Eq 10) $A_{1,2}F_{1,2-3,4} = A_{1,2}F_{1,2-3}-A_2F_{2-3}+A_1F_{1-4} + A_2F_{2-3,4}$
Notice in equation 10 that all of the shape factors can be found using the shape factor graph for perpendicular rectangles that share a common edge except for F1-4 which is the shape factor of interest. To find that shape factor solve equation 10 for F1-4. This will result in the following equation.
(Eq 11) $F_{1-4} = \frac{1}{A_1}[A_{1,2}F_{1.2-3.4}+A_2F_{2-3}-A_{1,2}F_{1,2-3}-A_2F_{2-3,4}]$