The easiest method to calculate radiative heat transfer between two bodies is when they are assumed to be black bodies. However, in reality most surface are grey bodies. Recall that grey bodies absorb a certain amount of radiation while reflecting a portion of the radiation off of the surface back into space. Refer to the image below.
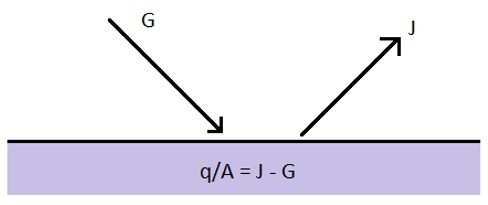
In the above image G represent irradiation which is the total radiation that come in contact with a surface per unit time and unit area. While J represents the radiosity which is the total amount of radiation that is reflected off a surface per unit time and unit area. The equation below can be used to determine the value for J.
(Eq 1) $J=εE_b+(1-ε)G$
ε = The Emissivity of the Object
Eb The Energy Emitted from a Black Body
To determine the net energy leaving the surface you would need to find the difference between the radiosity and irradiation as seen in the equation below.
(Eq 2) $\frac{q}{A}=εE_b+(1-ε)G-G$
A = Surface Area
Solving equation 1 for G and implementing it into equation 2 will than yield the following equation.
(Eq 3) $q=\frac{E_b-J}{(1-ε)/εA}$
Finally, the radiative heat transfer for a grey body can be represented as a resistance as seen from the equation below.
(Eq 4) $R=\frac{(1-ε)}{εA}$
Equation 3 shows you how to calculate the total radiative heat transfer when thermal radiation strikes a grey body. It however does not consider how different grey bodies will react with each other. When dealing with multiple bodies you will have to determine the radiation shape factor. Refer to the equation below to see the heat transfer between two bodies when the radiation shape factor is considered. Note, I discuss in detail how to find the radiation shape factor in another article.
(Eq 5) $q_{1-2}=\frac{J_1-J_2}{1/A_1F_{1-2}}$
F1-2 = The Shape Factor between surface 1 and 2
The equation to determine the resistance to radiative heat transfer for the radiation shape factor can be seen below.
(Eq 6) $R=\frac{1}{A_1F_{1-2}}$
Now what if you have two surfaces that are grey bodies that see only each other and nothing else? The image below represents the thermal resistances within the system.
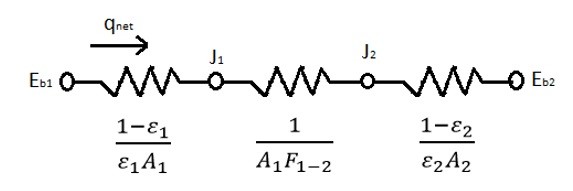
Finally, the equation below represents the total heat transfer between the two surfaces for the system where you have two grey bodies that only see each other.
(Eq 7) $q_{net}=\frac{σ(T_1^4-T_2^4)}{\frac{1-ε_1}{ε_1A_1}+\frac{1}{A_1F_{1-2}}+\frac{1-ε_2}{ε_2A_2}}$
σ = 5.669 X 10-8 W/m2-K4
Now what if you have two grey bodies radiating heat between each other and also radiating heat into a large room? This problem would be represented by the resistance diagram below.
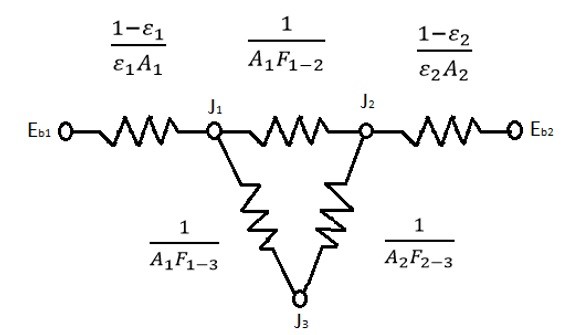
(Eq 8) $E_{b1} = σT_1^4$
(Eq 9) $E_{b2} = σT_2^4$
(Eq 10) $E_{b3} = σT_3^4 = J_3$
To determine the radiositie at J1 and J2 the following equations would be used.
(Eq 11) $ \frac{E_{b1}-J_1}{(1-ε_1)/ε_1A_1}+\frac{J_2-J_1}{1/A_1F_{1-2}}+\frac{J_3-J_1}{1/A_1F_{1-3}}=0$
(Eq 12) $\frac{J_1-J_2}{1/A_1F_{1-2}}+\frac{J_3-J_2}{1/A_2F_{2-3}}+\frac{E_{b2}-J_2}{(1-ε_2)/ε_2A_2}=0$
Next to find the total heat loss from object 1 the following equation would be used.
(Eq 13) $q_1=\frac{E{b1}-J_1}{(1-ε_1)/ε_1A_1}$
To find the total heat loss for object 2 the following equation would be used.
(Eq 14) $q_2=\frac{E_{b2}-J_2}{(1-ε_2)/ε_2A_2}$
To find the total heat transfer received by the room the following equation would be used.
(Eq 15) $q_3=\frac{J_1-J_3}{1/A_1F_{1-3}}+\frac{J_2-J_3}{1/A_2F_{23}}$
Finally, the net energy lost by the plates and then absorbed by the room would be represented by the following equation.
(Eq 16) $q_3=q_1+q_2$
As more and more surfaces are considered the more complex the problem will become.