In the previous section I talked about one dimensional conduction through a single type of material. However, this is not always the case. Sometime you will have conduction through materials that have different coefficients of thermal conductivity.
Now what if you have a multiple materials with different thermal conductivities as seen in the image below as seen in the image below.
(Eq 1) $q_x = -kA\frac{ΔT}{Δx}$
Now what if you have a multiple materials with different thermal conductivity as seen in the image below?
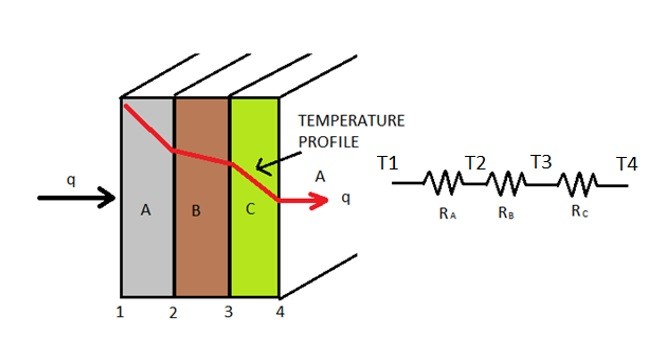
Taking the above image into consideration equation 1 can be modified to the following.
(Eq 2) $q = -k_AA\frac{T_2-T_1}{Δx_A} = -k_BA\frac{T_3-T_2}{Δx_B} = -k_CA\frac{T_4-T_3}{Δx_C}$
From equation 2 it can be seen that all three different materials of the above image will have the same heat flow going through them. This means that each of their individual thermal resistances are added up to a total system resistance. To calculate the individual thermal resistance for each material the following equation would be used.
(Eq 3) $R = \frac{Δx}{kA}$
For the above image, the individual resistances are in series to one another. To calculate the total resistance the following equation would be used.
(Eq 4) $R_{TOT} = R_A+R_B+R_C$
Now using the thermal resistances we can modify equations 1 and 2 to find the total heat transfer through the system. Refer to the equation below.
(Eq 5) $q = \frac{T_1-T_4}{R_{TOT}}$
Resistances can also be in parallel as seen in the image below.
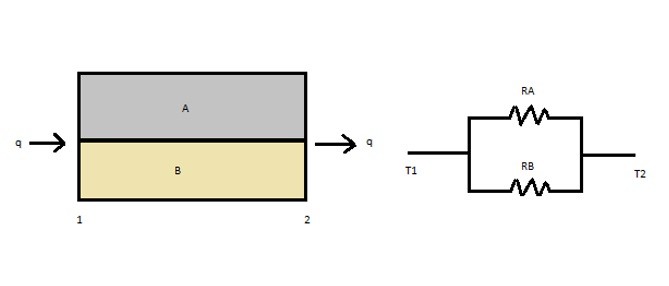
To calculate the total resistance for resistances in parallel the following equation would be used.
(Eq 6) $\frac{1}{R_{TOT}} = \frac{1}{R_A} + \frac{1}{R_B}$
There can also be combination components being in series and in parallel. Refer to the image below.
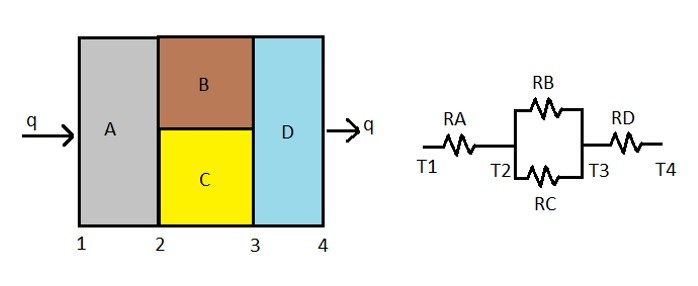
To calculate the total the resistance for the above image the following equation would be used.
(Eq 7) $R_{TOT} = R_A + \frac{R_BR_B}{R_B+R_C} + R_D$