Entropy is a thermodynamic property that is used to represent the unavailability of a systems thermal energy that cannot be converted into mechanical work. In turn, it shows that there is a degree of randomness in the system.
Entropy: Clausius Inequality
From the second law of thermodynamics it is known that there are expressions that involve inequalities. In turn, this will result in irreversible systems that are less efficient than reversible systems. As a result, this will lead us to the Clausius inequality which has major consequences in thermodynamics. The Clausius inequality was first stated by German physicist R. J. E. Clausius using the following cyclic integral expression.
(Eq 1) $\oint{}\frac{δQ}{T}≤0$
The above expression is valid for all reversible or irreversible cycles. In addition, this integral is performed over the entire cycle. As a result, the integral $δQ/T$ will be the sum of all the differential amounts of heat transfer that are divided by the temperature at the boundary.
Clausius Inequality Proof
The below image shows a system that is connected to a thermal reservoir that is at a constant absolute temperature $T_R$ through a reversible cyclic device. The thermal reservoir will provide heat, $δQ_R$, to the reversible cyclic device. In turn, the cyclic device will provide heat, $δQ$ to the system. In addition, the cyclic device will produce work $δW_{rev}, while the system will produce work $δW_{sys}$. The systems work is a result of heat transfer.
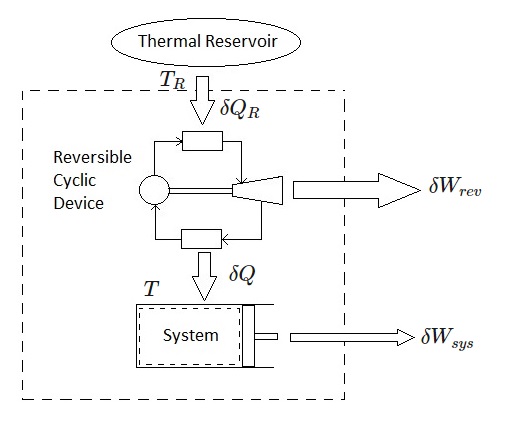
After applying the energy balance equation to the combined system, the following equation will result.
(Eq 2) $δW_c=δQ_R-dE_c$
where $δW_c=δW_{rev}+δW_{sys}$ and $dE_c$ is the total energy of the combined system.
Next, because the cyclic device is reversible the following equation will result.
(Eq 3) $\frac{δQ_R}{T_R}=\frac{Q}{T}$
Combining equations 2 and 3 will result in following equation.
(Eq 4) $W_c=T_R\frac{δQ}{T}-dE_c$
Finally, the system will undergo an integral number of cycles. In turn, equation 4 will become the following.
(Eq 5) $W_c=T_R\oint{}\frac{δQ}{T}$
In the above equation $W_c$ is the cyclic integral of $δW_c$. Also, it represents the net work for the combined cycle.
Currently it appears that the combined system is exchanging heat with a single reservoir while producing or consuming work $W_c$. However, we have to consider the the Kelvin-Planck statement. “No system can produce a net amount of work while operating in a cycle and exchanging heat with a single thermal energy reservoir.” As a result, $W_c$ cannot be a work output, which means it cannot be a positive quantity. Finally, $T_r$ is the thermodynamic temperature which is a positive quantity. Hence, we must have
$\oint{}\frac{δQ}{T}≤0$
Resulting in the Clausius inequality.
Clausius Inequality: Irreversible and Reversible Cycles
For a cycle to be internally reversible there must not be any irreversibilities within the system. This means that the cycle can be reversed. As a result, all of the quantities within the system would have the same magnitude with the opposite sign. Due to this, $W_c$ would have a negative quantity in the reversed case if it has a positive quantity in the regular case. Hence, $W_{c,int~rev} =0$ since it cannot be a positive or negative quantity. In turn, for a reversible cycle Clausius inequality will become the following.
(Eq 6) $\oint{}\left(\frac{δQ}{T}\right)_{int~rev}=0$
This equation concludes “the equality in the Clausius inequality holds for totally or just internally reversible cycles and the inequality for the irreversible ones.”
Entropy
Next, equation 2 allows us to develop a relation for the definition of entropy. First, we have to consider a quantity that’s cyclic integral is zero. An example of this would be a piston-cylinder device that is filled with a gas. In this case the piston will return to its initial position at the end of the cycle. As a result, the volume of the gas will also return to its initial value. Hence the net change in volume will be zero for the cycle. This is expressed as the following.
(Eq 7) $\oint{}d∨=0$
This means that the cyclic integral of volume is zero. However, if a quantity that has a cyclic integral of zero depends on state only, it does not consider the process path, which means it is a property. As a result, $(δQ/T)_{int~rev}$ represent a property in the differential form. This property is entropy. It is designated as $S$ and represented by the following equation.
(Eq 8) $dS=\left(\frac{δQ}{T}\right)_{int~rev}$ (kJ/K)
Entropy is an extensive property. In addition, entropy is sometimes referred to as total entropy of a system. During a process the entropy change can be determined by integrating equation 8.
(Eq 9) $ΔS=S_2-S_1=\int{^2_1}\left(\frac{δQ}{T}\right)_{int~rev}$ (kJ/K)
Isothermal Heat Transfer
An isothermal heat transfer process is an internally reversible process. As a result, the change in entropy for the system can be determined by performing the following integration.
(Eq 10) $ΔS=\int{^2_1}\left(\frac{δQ}{T}\right)_{int~rev}$$=\int{^2_1}\left(\frac{δQ}{T_o}\right)_{int~rev}$$=\frac{1}{T_o}\int{^2_1}(δQ)_{int~rev}$
or
$ΔS=\frac{Q}{T_o}$ (kJ/K)
In the above equation $T_o$ is the constant temperature of the system and $Q$ represents the heat transfer.