When there is an interface between a liquid or gas, or between two immiscible fluids such as oil and water, forces will develop on the surface of the liquid. The force that develops on the surface of the liquid causes the fluid’s surface to act like a skin. This is known as surface tension. For example if you were to gently place a steel needle onto the surface of water it will float instead sink. This is due to the surface tension of the water.
Surface tension is a phenomena caused by unbalanced cohesive forces that are acting on the liquid molecules that are on the surface. The reason why this happens is because of the following. First, let’s take a look at the fluids molecules inside the liquid. These molecules are attracted to each other equally on all sides causing a net force of zero. On the other hand the molecules on the surface of the liquid are subjected to a net forced caused by the molecules on the interior of the liquid. Since there is an unbalanced force on the fluid molecules on the surface of a liquid a surface tension develops.
Surface tension is represented by the Greek letter σ with the following dimensional units $FL^{-1}$. The surface tension is temperature dependent, where it normally decreases as temperature increases.
Surface Tension of Common Liquids in Contact with Air
|
Liquid |
Temperature |
Surface Tension |
||
|
Fahrenheit |
Celsius |
$lb/ft$ |
$N/m$ |
|
|
Ethyl Alcohol |
68 |
20 |
1.56e-3 |
2.28e-2 |
|
Gasoline |
60 |
15.6 |
1.50e-3 |
2.2e-2 |
|
Mercury |
68 |
20 |
3.19e-2 |
4.66e-1 |
|
SAE 30 oil |
60 |
15.6 |
2.5e-3 |
3.60e-2 |
|
Sea Water |
60 |
15.6 |
5.03e-3 |
7.34e-2 |
|
Water |
60 |
15.6 |
5.03e-3 |
7.34e-2 |
Pressure Inside a Drop of Fluid
If you had drop of fluid floating in space there would be pressure within that fluid droplet due to the cohesive forces between the molecules of the fluid. Those cohesive forces create a surface tension that will hold the fluid together. To determine the pressure inside the droplet the following free body diagram would be used.
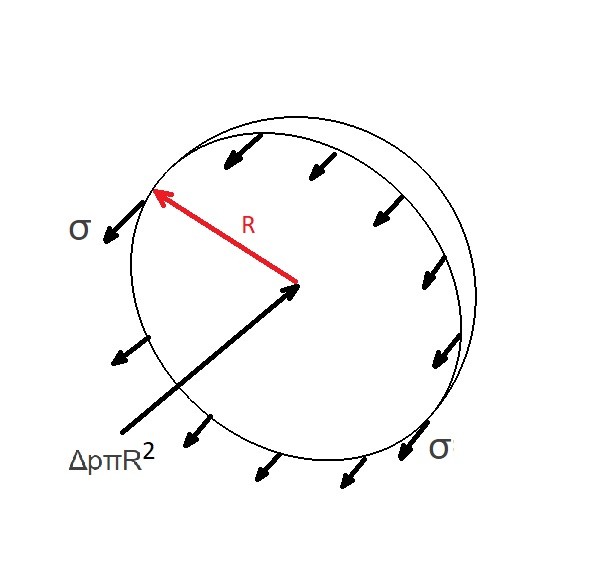
(Eq 1) $2πRσ=ΔpπR^2$
or
$Δp=\frac{2σ}{R}=p_i-p_e$
where
$σ$ = surface tension
$R$ = radius
For the equations above $Δp$ represents the pressure difference between the outside pressure $p_e$ on the droplet and the pressure inside the droplet $p_i$.
Surface Tension in a Small Tube
If you were to place a capillary tube into a liquid you will notice that the liquid will rise and fall with the tube to a certain extent. This is cause by the attraction between the wall of the tube and the liquid’s molecules overcoming the attraction between the liquid molecules towards each other in the fluid. This known as wetting the solid surface.
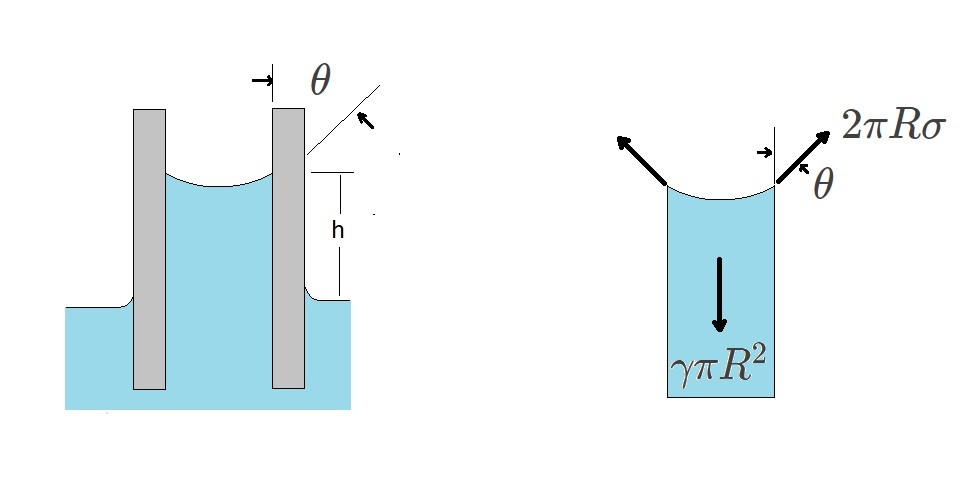
(Eq 2) $γπR^2h=2πRσcosθ$
or
$h=\frac{2σcosθ}{γR}$
where
$γ$ = specific weight
From the above equations it can be seen that as the tube’s radius becomes smaller the liquid height will increase. Finally, the angle of contact between liquid and the surface can be based off of how clean the surface of the tube is. If glass tube is used that has a perfectly clean surface than θ will be approximately equal to zero.